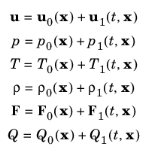where the subscript “1” variables represent the acoustic perturbations (first-order perturbation) and subscript “0” the background mean flow quantities. Assuming zero mean flow u0 = 0 and after inserting into the governing Equation 6-4, the steady-state equations can be subtracted from the system, which is subsequently linearized to first order by ignoring terms quadratic in the acoustic variables. Dropping the subscript “1” for readability yields the thermoviscous acoustic equations:

The density ρ is expressed in terms of the pressure and the temperature variations using the density differential (Taylor expansion about the steady quiescent values)

The two thermodynamic quantities (the coefficient terms in square brackets) define the isobaric coefficient of thermal expansion αp (sometimes named α0) and the isothermal compressibility βT, according to the following relations

where Ks is the isentropic bulk modulus (sometimes named K0), KT the isothermal bulk modulus, Cv is the heat capacity at constant volume (per unit mass), c is the (isentropic) speed of sound, and γ is the ratio of specific heats (the adiabatic index). The isothermal compressibility βT is related to the isentropic (or adiabatic) compressibility βs (sometimes named β0) and the coefficient of thermal expansion αp via the thermodynamic relations

It is derived using the Maxwell relations; see, for example, Ref. 5 and Ref. 7.

From Equation 6-7 and Equation 6-8 the isothermal compressibility and the isobaric coefficient of thermal expansion can be expressed in terms of the speed of sound as

The equations presented in Equation 6-5 and Equation 6-6 are the ones solved in the time domain in The Thermoviscous Acoustics, Transient Interface. Assuming small harmonic oscillations about a steady-state solution, the dependent variables and sources can be assumed to take on the following form

Inserting this into the governing equations and performing the linearization yield the equations solved in the frequency domain in The Thermoviscous Acoustics, Frequency Domain Interface:

The system of equations implemented in the thermoviscous acoustics interfaces is further given in a scattered field formulation, as described below in Scattered Field Formulation and Background Acoustic Fields.

When the Adiabatic formulation option under the Thermoviscous Acoustics Equation Settings section the solved equations reduce to:

where the temperature T depends directly on the acoustic pressure p.

For an ideal gas, the equation of state p = ρRT, where R is the specific gas constant, leads to

Inserting these expressions and dividing the continuity equation by the reference density, Equation 6-10 in the frequency domain take on the following simplified form

where we have assumed constant background properties. Defining the speed of sound c in analogy with the standard assumptions for linear acoustics (term in front of the pressure in the continuity equation), it is found that

In the case with a general fluid, the corresponding relation is using Equation 6-7 and Equation 6-8:

where K0 is the adiabatic bulk modulus, KT the isothermal bulk modulus, and α0 the coefficient of thermal expansion.

If the thermodynamic processes in the system are assumed to be adiabatic and viscosity can be neglected Equation 6-12 reduces, for constant background properties, to