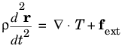where ρ is the density,
r denotes the coordinates of a material point,
T is the stress tensor, and
fext is an external volume force such as gravity (
fext = ρg). This is the equation solved in the structural mechanics interfaces for the special case of a linear elastic material, neglecting the electromagnetic contributions.
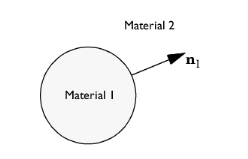
where T1 and
T2 represent the stress tensor in Materials 1 and 2, respectively, and
n1 is the normal pointing out from the domain containing Material 1. This relation gives rise to a surface force acting on the boundary between Material 1 and 2.
In certain cases, the stress tensor T can be divided into one part that depends on the electromagnetic field quantities and one part that is the mechanical stress tensor,