Frequency Domain
Phasors
Whenever a problem is time harmonic the fields can be written in the form
Instead of using a cosine function for the time dependence, it is more convenient to use an exponential function, by writing the field as
The field 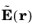is a phasor, which contains amplitude and phase information of the field but is independent of t.
Frequency Domain Formulation
With the use of phasors, Maxwell’s equations can be formulated in the frequency domain. One of the main advantages is that a time derivative corresponds to a multiplication by jω:
If the fields satisfy a linear time-dependent equation, then the corresponding phasors must satisfy a similar equation in which the time derivatives are replaced by a factor jω. In this way, linear differential equations are converted to algebraic equations that are much easier to solve.
For sake of simplicity, when writing variables and equations in the frequency domain, the tilde is dropped from the variable denoting the phasor. However, it is important to remember that the field that has been calculated is a phasor and not a physical field. Also note that the phasor is visualized in the plot as by default, which is E at time t = 0. To obtain the solution at a given time, specify a phase factor in all results settings and in the corresponding functions.
The frequency domain formulation is only applicable for equations linear in the fields and for one specific frequency. In general, it cannot be used with materials whose properties depend on the fields themselves. To model such nonlinear materials with the frequency domain formulation, different approaches are required. See Effective Nonlinear Magnetic Constitutive Relations for a formulation that approximates nonlinear magnetic constitutive relations in time-harmonic problems.
Sign Convention
The time dependency of a time-harmonic field can be written in two ways: ejωt or e−jωt. In COMSOL Multiphysics, the former sign convention ejωt is used.
The time-harmonic sign convention dictates the sign convention for some material coefficients in the frequency domain, such as complex permittivity, complex permeability, and complex refractive index. For example, in the dielectric loss model, the complex relative permittivity is defined as
where ε' and ε'' are two material parameters that are named as the real part and imaginary part of the relative permittivity, respectively. Inserting the complex relative permittivity in the frequency domain Maxwell–Ampère’s law gives
where the term ωε0ε'' contributes to energy loss that is indistinguishable from the loss quantified by the electrical conductivity σ. With the sign convention used here, a positive material parameter ε'' corresponds to a loss although the imaginary part of the complex number ε' – jε'', evaluated as imag(ε' – jε''), is negative. See Modeling Losses in the Frequency Domain for details.