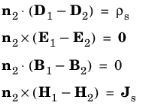where ρs and
Js denote surface charge density and surface current density, respectively, and
n2 is the outward normal from medium two.

A perfect conductor has infinite electrical conductivity and thus no internal electric field. Otherwise, it would produce an infinite current density according to the third fundamental constitutive relation. At an interface between a dielectric and a perfect conductor, the boundary conditions for the E and
D fields are simplified. Assume that subscript 1 corresponds to a perfect conductor; then
D1 = 0 and
E1 = 0 in the relationships just given. If it is a time-varying case, then
B1 = 0 and
H1 = 0 as well, as a consequence of Maxwell’s equations. The result is the following set of boundary conditions for the fields in the dielectric medium for the time-varying case: