Gaussian Beams as Background Fields and Input Fields

When solving for the scattered field, the background wave type can be set to a predefined Gaussian beam from within the of The Electromagnetic Waves, Frequency Domain Interface. Additionally, Gaussian beams can be specified as the input field for the Scattering Boundary Condition and the Matched Boundary Condition.

In the paraxial approximation, the field for a Gaussian beam propagating along the z-axis is

where w0 is the beam radius, p0 is the focal plane on the z-axis, EG0 is the Gaussian beam electric field amplitude, and the spot radius for different positions along the propagation axis is given by

defines the radius of curvature for the phase of the field and the so-called Gouy phase shift is given by

The equations above are expressed using the Rayleigh range z0 and the transverse coordinate ρ, defined by

Note that the time-harmonic ansatz in COMSOL Multiphysics is ejωt, and with this convention, the beam above propagates in the +z direction. The equations are modified accordingly for beams propagating along the other coordinate axes.

The field for a Gaussian beam is defined in a similar way for 2D components. In the particular case where the beam propagates along the x-axis, the field is defined as

For a beam propagating along the y-axis, the coordinates x and y are interchanged.

Notice that the expressions above for Gaussian beams are not solutions to the Helmholtz equation, but to the so called paraxial approximation of the Helmholtz equation. This means that these equations become less accurate the smaller the spot radius is and should not be used when the spot radius is of the same size as or smaller than the wavelength.

To circumvent the problem that the paraxial approximation formula is not a solution to the Helmholtz equation, a plane wave expansion can be used to approximate a Gaussian beam background field. Since each plane wave is a solution to Helmholtz equation, also the expansion is a solution to Helmholtz equation.

The plane wave expansion approximates the Gaussian distribution in the focal plane

where the beam is assumed to be propagating in the z direction, the focal plane is spanned by the x- and y-coordinates, e is the unit magnitude transverse polarization in the focal plane, l and m denote the indices for the wave vectors, the index n accounts for the two polarizations per wave vector klm, almn is the amplitude, un(klm) is the unit magnitude polarization, and r is the position vector.

Multiplying with the conjugate of the exponential factor above and the polarization factor un(klm) and applying a surface integral over the entire focal plane allows us to extract the amplitudes as

where kt,lm is the magnitude of the transverse wave vector component.
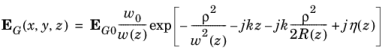