Richards’ equation appears deceptively similar to the saturated flow equation set out in the Darcy’s Law interface, but it is notoriously nonlinear (Ref. 3). Nonlinearities arise because the material and hydraulic properties
θl,
Se,
Cm, and
κr vary for unsaturated conditions (for example, negative pressure) and reach a constant value at saturation (for example, pressure of zero or above). The volume of liquid per porous medium volume,
θl, ranges from a small residual value
θr to the total porosity
εp. Its value is given in a constitutive relation in the model commonly defined as:
The variable θs is the saturated liquid volume fraction and therefore
θs =
εp. The effective saturation,
Se has a maximum value of 1 at saturation and usually follows a nonlinear relationship if the porous medium is unsaturated. The specific moisture capacity,
Cm, describes the change in
θl as the solution progresses, the slope on a plot of
θl versus pressure (or pressure head):
The relative permeability, κr, increases with moisture content and varies from a nominal value to 1 at saturation, which reveals that the fluid moves more readily when the porous medium is fully wet.
The analytic formulas of van Genuchten (Ref. 4) and Brooks and Corey (
Ref. 5) are so frequently used that they are synonymous with this variably saturated flow modeling. Posed in terms of pressure head
Hp = p/(ρ g), the analytic expressions require data for the saturated
θs and residual
θr liquid volume fractions as well as constants
α,
n,
m, and
l, which specify a particular medium type.
For the liquid volume fraction Equation 4-20 is used. The relative permeability is defined as
which results in κr = 1 at saturation (
Se = 1). The specific moisture capacity is defined as:
here, the constitutive parameter m is equal to
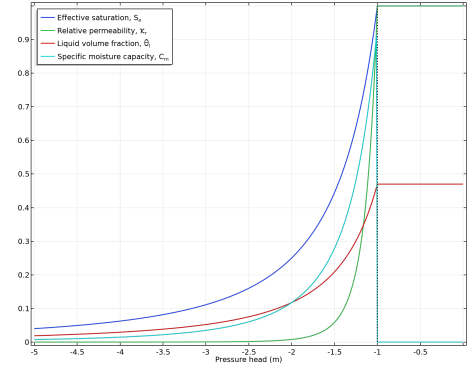
1 − 1 / n. The functions are highly nonlinear which is also depicted in
Figure 4-2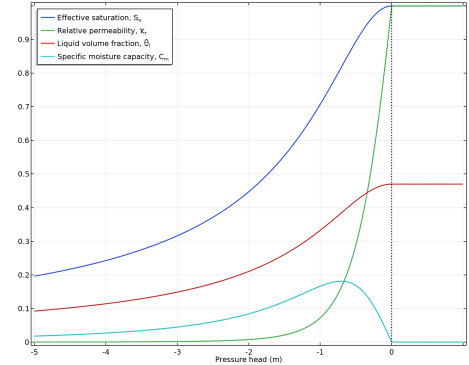
Again Equation 4-20 describes the liquid volume fraction. The relative permeability is defined as
which results in κr = 1 at saturation (
Se = 1). The specific moisture capacity is defined as:
Here, the constitutive parameter m is equal to
1 − 1 / n. The functions are highly nonlinear which is also depicted in
Figure 4-3