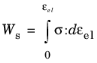Elastic Energy
Linear Elastic Materials
The elastic energy is defined as the recoverable energy stored in an elastic material or spring. The elastic strain energy density in an elastic material is defined as
(3-204)
If the linear elasticity is assumed, then
where σi is the initial stress. The integration can then be carried out analytically and the result is
This expression is used for the Linear Elastic Material model in a Stationary or Time Dependent analysis. An implication is that if you modify the linear elastic model in a way that violates the assumption about stress-strain linearity above, then the computed strain energy density may be wrong, for example, using a strain dependent Young’s modulus or a nonconstant initial stress.
In the case of Frequency Domain analysis, only the harmonic part is considered. That is, a constant prestress does not contribute to the strain energy density. To emphasize this, the concept of stored energy is used. The stored energy is the cycle average of the elastic energy; that is,
The harmonic stress and strain components are generally not in phase with each other, so the cycle average of the stored energy is computed as
where the stress and strain are considered as complex quantities, and the overline denotes a complex conjugate.
Hyperelastic Materials
For a Hyperelastic material, the strain energy density function is the fundamental quantity from which stresses are derived. The form of the strain energy density function is determined by the hyperelastic model used.
Nonlinear Elastic Materials
For a Nonlinear Elastic Material, the strain energy density is computed in different ways depending on the material model selected. If the integration in Equation 3-204 can be performed analytically, then a closed form expression is used, similar to what is done in the linear elastic material. If not, then the integral is actually computed using the integrate() operator.
Structural Elements
For structural elements, the strain energy density is split into membrane, bending and shear parts, which are then summed into a total strain energy density.
The strain energy density for all elastic domains are integrated to give a total elastic strain energy, which contains all elastic energy stored in a certain physics interface.
Elastic boundary conditions, such as Spring Foundation, Thin Elastic Layer, and Springs in joints in the Multibody Dynamics interface, also contribute to the total elastic strain energy variable. In these cases, linearity is assumed, so if you enter nonlinear data, you will probably need to adjust the strain energy expressions.
The Multibody Dynamics interface is available with the Multibody Dynamics Module.