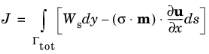where Ws is the strain energy density,
σ is a stress tensor, and
m is the outward normal of the integration contour
Γ. In
Equation 3-198, the crack is assumed to extend in the positive
x direction, and integration is made over
, which can be any closed path around crack tip, see
Figure 3-39. However, if there is no loading on the crack face, the contribution to
J on
Γface is zero, and it is sufficient to only perform the integration over
Γ.
In 3D, the path integral can be taken around an arbitrary point of the crack front, and Γtot can be any closed path around the point in the normal plane to the crack front. It then turns out that there is also an additional term, to be integrated over the area enclosed by
Γtot. The expression is then further extended to
where t is the tangent to the crack front. In practice, this is also the normal to the plane of the integration contour.
In 2D axisymmetry, m and
p are located in the
rz-plane, and
t is oriented in the azimuthal direction. The surface integral can then be simplified, so that
where er is the base vector of the global
r direction.
When a boundary load FA is applied on the crack face, it contributes with an additional term to the J-integral since the contour integrals on the crack face become nonzero. This additional contribution,
Jface, is defined by
where Γface is schematically defined in
Figure 3-39.
where Eeff is an effective Young’s modulus that accounts for the stress state at the crack front. Assuming that
KII =
βKI and
KIII =
γKI / (1 +
ν), where
β and
γ are coefficients that account for the mode mixture, it follows from
Equation 3-199 that the stress intensity factors are
where ΔuI,
ΔuII, and
ΔuIII are the components of the displacement vector across the crack,
Δu, defined in the coordinate system corresponding to the three modes of fracture.