Consider a mass-spring-damper system, attached to a moving base. The base movement is b(t).

It can be seen that the support movement acts as a forcing term, and that the solution depends only on two parameters ω0 and ζ, and not on the individual values of m, c, and k.

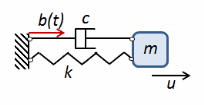
For given values of ω0, ζ, and b(t), it is a trivial task to solve Equation 3-150 for the whole duration of the event plus some extra time to allow for the response to reach a possible maximum. The acceleration, velocity, and displacement response spectra are defined as

These are absolute spectra. One can do a similar definition of the relative spectra by using instead the relative displacement ur. It is clear from the definition that there is not a one-to-one relation between the response spectrum and the base acceleration history. The response spectrum gives information about the peak value, but not about when it occurs.

Let b(t) be a vector that has the same size as the displacement vector u (the total number of DOF), but it contains only three different values: bx(t) in all x-translation DOFs, by(t) in all y-translation DOF, and bz(t) in all z-translation DOF. The relative displacement is now ur = u − b. With no external load, Equation 3-151 can be written as

The equation is similar to the standard SDOF system in Equation 3-150.

In Equation 3-152, qj is the modal coordinate for mode j, so that the relative displacement can be written as a superposition of the eigenmodes .

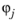
The notation 1x mean a vector that has the value 1 in all DOF representing x-translation, and the value 0 in all other DOF. Inserting Equation 3-153 in Equation 3-152 gives

The multipliers Γkj are the modal participation factors defined as

Thus, the maximum amplitude of mode j, when loaded by a base motion described by a response spectrum in direction k, is

The general approach is to consider the excitation in three directions, I, (I = 1,2,3) separately. First all modal responses are summed for each direction, and then the results for the three directions are summed. Some methods, however, do both combinations in one sweep.

In a high frequency mode, the mass of the SDOF oscillator will mainly be translated in phase with the support. Such modes constitute the rigid modes. Their responses are synchronous with each other (and with the base motion). This means that for rigid modes, a pure summation should be used, since they are fully correlated.

In addition, it is sometimes necessary to add some static load cases, containing a missing mass correction. The reason is that when only a limited set of eigenmodes is used in the superposition, those modes do not represent the total mass of the structure.

In the following, RI denotes any result quantity caused by excitation in direction I. RI can be for example be displacement, velocity, acceleration, strain component, stress component, equivalent stress, or a beam section force. The periodic part of RI is denoted RpI, and the rigid part is denoted RrI. Similarly, RpI,j and RrI,j denote the results from an individual eigenmode j.

There are two different methods in use, by which the partitioning can be done. In either case, for mode j,

The difference between the two methods lies in how the coefficients αj are determined. For low frequencies, it should approach the value 0 (fully periodic modes). And for high frequencies, the value is 1 (fully correlated rigid modes).

In the Gupta method, αj is a linear function of the logarithm of the natural frequency.

where f1 and f2 are two key frequencies. Thus, for eigenfrequencies below f1, the modes are considered as purely periodic, and above f2 as purely rigid. In the original Gupta method, the lower key frequency is given by

where Sa,max and Sv,max are the maximum values of the acceleration and velocity spectra, respectively. In the idealized spectrum shown in Figure 3-31, this exactly matches the point D.

In the Lindley–Yow method, the coefficient αj depends directly on the response spectrum values, and not only on the frequency. As a consequence, it is possible that a certain mode can be considered as having a different degree of rigidness for different excitation directions

The so-called zero period acceleration (ZPA) is the maximum ground acceleration during the event

This is the high frequency asymptotic value of the absolute acceleration (or pseudoacceleration). It also corresponds to the F-G part of the spectrum in Figure 3-31.

The value of αj must be in the range from 0 to 1, and it must increase with frequency. For this reason, NRC RG 1.92 requires that αj must be set to zero for any eigenmodes below point C in Figure 3-31. For a general spectrum, this is implemented as a strict requirement that αj has a monotonous decrease with decreasing frequency from fZPA. As soon as an increase in αj is found, the value is set to zero for all lower frequencies.

All summation rules for periodic modes except Absolute Value Sum can be summarized by the following expression:

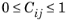
Here, RpI is the total periodic response of some result quantity R with respect to excitation in direction I (I=1,2,3). RpI,j is the result from an individual eigenmode j, and N modes are used in the summation. The interaction between the modes is determined by the coefficient Cij (). The different evaluation methods vary only in the definition of Cij.

Since Cij is symmetric and Cij = 1 when i = j, it is more efficient to use the expression

The result quantity R is computed using the ordinary definitions of how a variable is obtained from the DOF fields. This can be expressed as R = g(u). The operator g is however applied to the mode shape, multiplied by a scalar (spectrum value times participation factor)

where ζi is the modal damping. In the implementation in COMSOL Multiphysics, all modes are assumed to have the same damping.

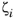
where td is a separate input, called the time of duration. The value of differs between modes, even though the damping is constant.

This method, which is often called complete quadratic combination (CQC), is similar to the previous double sum method. The general expression contains modal damping values. Given that a single damping value is used here, the mode correlation expression can be simplified to

where Rmm,I is the term for the missing mass correction, if used.

In general, a mode superposition using a limited number of modes will miss some mass. With the assumption that the higher order modes do not have any dynamic amplification, it is possible to device a correction by solving some extra static load cases, containing the acceleration excitation acting on the 'lost' mass. So-called static correction can be used for mode superposition in general. For the case of response spectrum analysis, the expressions are somewhat simplified.

In terms of the assembled finite element equations, the static correction load fc can be written as

Here, f is the original load vector, M is the mass matrix, and rk are the modal loads, given by the projection of the load vector on the eigenmodes ,

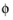
To actually compute the load in Equation 3-155, the participation factors from a corresponding eigenfrequency study step are needed. The structure of the load is similar to that of a gravity load, but with the acceleration of gravity replaced by the space-dependent field

The load is implemented by using Gravity nodes in the Structural Mechanics interface. The sum of the products between participation factors and mode shapes is performed in a Combined Solutions study step.

In this method, there is no need to deduce the actual missing mass. It can only be used together with the Lindley–Yow method. According to the Lindley–Yow method, all rigid modes have acceleration SZPA. This acceleration is given to the whole structure. The static load cases are thus just pure gravity loads, but scaled by SZPA instead of the acceleration of gravity.

where the Der Kiureghian expression Equation 3-154 for Cij is used.

It is now conceptually assumed that the response spectra are instead applied in a local coordinate system X'-Y' which is rotated an angle θ with respect to the X-Y orientations. It can then be shown that

the same ratio γ will apply to the responses. The peak response as function of the rotation angle is obtained by an SRSS type summation

It can be seen that for γ = 1, the standard SRSS expression is retrieved.

The angle θmax giving the maximum response R(θmax) turns out to be independent of γ, and it has the value

There are two roots for θmax, both of which must be checked.

Now, it is possible to have the rigid modes too in a CQC3 context. Another way of expressing this is that the rigid response is treated as mode N + 1, the summation in the CQC3 rule is extended to N + 1, and

In the GUI, this extension is selected by checking the Augment with rigid response check box.

It retains the property of selecting the worst orientation, through the search for θmax. The extension to rigid modes is the same as for CQC3.