Equation Implementation
The equilibrium equations for solid mechanics are given by Newton’s second law. It is usually written using a spatial formulation in terms of the Cauchy stress tensor σ:
Here fV is a body force per unit deformed volume, and ρ is the current mass density. For the material frame formulation used in COMSOL Multiphysics, it is more appropriate to use a Lagrangian version if the equation:
Now that the first Piola–Kirchhoff stress tensor, P, is used. FV is a body force with components in the current configuration but given with respect to the undeformed volume, and ρ0 is the initial mass density. Note the gradient operators are not the same: in the first case the gradient is taken with respect to the spatial coordinates, and in the second case with respect to the material coordinates. Using the more common second Piola–Kirchhoff stress tensor, S, the same equation reads
(3-148)
where F is the deformation gradient. The COMSOL Multiphysics implementation of the equations in the Solid Mechanics interface is however not based on the equation of motion directly, but rather on the principle of virtual work.
The principle of virtual work states that the sum of the internal virtual work and the external virtual work are equal. The internal virtual work is the work done by the current stress state on a kinematically admissible variation in strains. The external virtual work is the work done by all forces (acting on domains, boundaries, edges, or points) when multiplied with the variation in displacements corresponding to the variation in strains. The virtual displacements δu are in the finite element formulation represented by the test() operator in COMSOL Multiphysics. For a stationary case, the virtual work δW is written as
The strains are computed from the gradients of the displacements, and the stresses are given by the constitutive relation.
In a dynamic analysis, the inertial forces are included in the volume forces, according to d’Alembert’s principle.
(3-149)
Since the equations are formulated on the material frame, all integrals are taken over the undeformed geometry. The stress and strain contributions must be interpreted differently depending on whether the formulation is geometrically nonlinear or not.
•
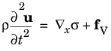
If the study step is geometrically linear, the strain ε is the engineering strain. The stress σ could in principle be any of the stress measures, as they all converge to the same engineering stress in this case.
•
If the study step is geometrically nonlinear, the variation of strain δε is taken from the displacement gradient, and the stress conjugate σ is the first Piola–Kirchhoff stress. The integration is done in the undeformed configuration.
The Solid Mechanics interface supports Stationary (static), Eigenfrequency, Time Dependent (transient), Frequency Domain, and Modal solver study types as well as linear buckling.