Shape Memory Alloy

The term shape memory alloy (SMA) normally refers to alloys that can undergo large strains, effect called superelasticity or pseudoelasticity; and also to materials that after undergoing large deformations can remember their original shape when heated above a certain temperature.

These alloys are mixtures of metals such as copper, aluminum, nickel, titanium and other. Nickel-titanium (NiTi) alloys have applications in many industries due to their thermal and mechanical properties. Most of the industrial applications of NiTi alloys take advantage of the different mechanical properties of the two crystalline structures found around room temperature: austenite and martensite.

Hot NiTi alloys are composed by a pure austenite phase. The martensite phase develops upon cooling the alloy below the martensite start temperature, Ms. The martensite volume fraction ξM will increase until the cooling temperature reaches the martensite finish temperature, Mf, below which the alloy microstructure will be pure martensite.

The reverse process has different transition temperatures: A pure martensite alloy will develop an austenite microstructure if it is heated above the austenite start temperature, As. The austenite phase will increase upon heating the material to the austenite finish temperature, Af, above which the alloy microstructure becomes 100% austenite.

Many industrial applications take advantage of this hysteresis loop, as the transition temperatures are not the same in a heating-cooling cycle.

There are two shape memory alloy models available with the Nonlinear Structural Material Module: the Souza–Auricchio model and the Lagoudas model. These material models differ in the expression for the free energy density.

For the Souza–Auricchio model, Helmholtz free energy density depends on two state variables: the total strain tensor ε and the temperature T. An additional internal variable is used to compute the transformation strain tensor εtr (Ref. 33-34)

here, c is the heat capacity at constant pressure, K and G are the bulk and shear moduli, εvol is the volumetric strain, Hk is the hardening modulus, and I(εtr) is the indicator function for the strain limit constraint. The equivalent transformation strain εtre is used as a measure of the transformation strain tensor

The indicator function is defined by

The term ψch = f(T)|εtr| is denoted as the chemical energy density due to the thermally induced martensite transformation. The function f(T) corresponds to the temperature-dependent martensite to austenite equilibrium stress, defined from the slope of the limit curve β and the reference temperature T*

Here, the operator < > denotes the Macaulay brackets.

The conjugated thermodynamic stress σtr associated to the transformation strain variable is

The evolution of the transformation strain εtr is given by the so-called limit function, which takes the same form as the yield function for metal plasticity.

The evolution equation for the transformation strain εtr is computed from the flow rule

where the plastic multiplier λp is solved with the Kuhn–Tucker conditions, as done for plasticity, see Plastic Flow for Small Strains.

For Lagoudas model, Gibbs free energy density depends on two state variables: the total stress tensor σ and the temperature field T. Additional internal variables are used to compute the transformation strain tensor εtr and the martensite volume fraction ξ (Ref. 35)

Here, c is the heat capacity at constant pressure, s0 is the specific entropy at reference state, S is the compliance matrix, εth is the thermal strain tensor, εtr is the transformation strain tensor, u0 is the specific internal energy at reference state, and f(ξ) is the transformation hardening function. The compliance matrix S, is obtained by a volume average of the elastic properties of martensite and austenite

where ΔS = SM − SA. Also, other material parameters are averaged this way.

As opposed to Souza–Auricchio model, the evolution equation for the transformation strain εtr is computed from the flow rule

where the normalized transformation tensor Λ changes principal directions depending on the direction of the martensitic transformation.

The maximum transformation strain in Lagoudas model can be considered constant, or stress-dependent as described in Ref. 36. A stress-dependent maximum transformation strain can be used at low stress levels, where the martensite turns into detwinned structures.

The variable for the direction of the martensitic transformation,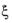

, is calculated from the previous state to determine the expected increment or decrement of the transformation strain tensor εtr. This calculation is computational expensive and it can lead to convergence issues. Since in many applications the transformation direction

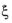
is known a priori (for instance, mechanical loading or unloading, or temperature increment/decrement) a user input enables to set the transformation direction manually to 1 or -1, thus speeding up the computational time.

For Lagoudas model, it is possible to choose from different transformation hardening functions f(ξ)

The quadratic hardening function is defined as

where the parameters bM and bA are computed from

and the parameters μ1 and μ2 from

The smooth hardening function is defined with four smoothing parameters n1, n2, n3, and n4:

In Lagoudas model, the phase transformation is described by six parameters: the transition temperatures Ms, Mf, As, Af, and the two slopes of austenite and martensite limit curves CA and CM.

When the experimental data consists of a uniaxial stress-strain curve taken at constant temperature, it is handy to enter the transition stress levels instead of the transition temperatures.

Consider a NiTi alloys at constant temperature composed by 100% of austenite volume fraction. Upon loading, the slope in the stress-strain curve would be the Young’s modulus of austenite, EA. The martensite phase starts to develop when the axial stress reaches the martensite start stress, σMs. If the alloy is further loaded, the slope reduces, entering a region called loading plateau. Above the martensite finish stress, σMf, the microstructure becomes 100% martensite. This process is commonly called the forward transformation.

The reverse process has different transition stresses: If the 100% martensite alloy is unloaded, the slope follows the martensite Young’s modulus EM. When the axial stress reaches the austenite start stress, σAs, the austenite volume fraction ξA starts to develop until the axial stress falls below the austenite finish stress, σAf, at which level the alloy microstructure is 100% austenite. This process is commonly called the reverse transformation. Figure 3-26 illustrates this process.

The relations between the start and finish temperatures and stresses are

here, Tσ is the constant temperature at which the stress-strain curve was measured.

Since phase transformation is an inelastic process, the dissipated energy density can be calculated by integrating the pseudo-rate given by

For Souza-Auricchio model the dissipated energy density rate is then defined by

For Lagoudas model it is defined by

As plasticity is rate independent, the transformation dissipation density Wtr is obtained after integrating an extra variable in the plastic flow rule.