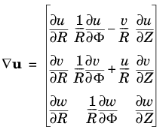Axial Symmetry
The 2D axisymmetric implementation in COMSOL Multiphysics by default assumes independence of the azimuthal component of the displacement. Therefore, the physical components of the radial and axial displacement, u and w, are used by default as dependent variables for the axially symmetric geometry. It is also possible to include the dependent variable v for the out-of-plane displacement, or an azimuthal mode extension in time-harmonic studies. See Circumferential Displacement and Circumferential Modes.
Strains
The displacement gradient with respect to the cylindrical coordinates of the undeformed geometry reads
The assumption of axial symmetry neglect gradients in the azimuthal direction, so the displacement vector is considered independent on the azimuthal angle, u = u(R, Z), and
.
The displacement gradient after this assumption reads
and the Green–Lagrange strain tensor is
Assuming that there is no torsion around the axis of symmetry, so there is no out-of-plane displacement, v = 0, the deformation gradient can be further simplified to read
For geometrically linear analysis, the nonlinear terms in the Green–Lagrange strain tensor are dropped
and the volumetric strain is computed from
For the 1D axisymmetric representation, only the radial component of the displacement field is computed, and only gradients with respect to the radial direction are considered, this is, u = u(R), and .
Circumferential Displacement
When the out-of-plane displacement is considered in a 2D axisymmetric model, torsion is allowed with respect to the symmetry axis. In this case, the displacement gradient reads
and the Green–Lagrange strain tensor is
For geometrically linear analysis, the nonlinear terms in the Green–Lagrange strain tensor are dropped
and the volumetric strain is computed from
Circumferential Modes
A standard 2D axisymmetric representation of the structure assumes the independence of the solution with respect to the azimuthal angle . The following 3D solution represents an extension of this assumption:
where m is a circumferential mode number (or azimuthal mode number) that can only have integer values to obey the axially symmetric nature of the corresponding 3D problem, that is, there is an azimuthal symmetry  =  + 2π. Thus,
The static prestress solution u0 can be obtained using a standard static analysis in 2D axially symmetric geometry; and the circumferential wave number km = m/R can be introduced to describe the circumferential modes.
The displacement vector u1 can have nonzero values in all three components, which are functions of the radial and axial positions. For a given circumferential mode number m, the displacement vector u1 can be found using an eigenfrequency analysis in a 2D axially symmetric geometry. Hence,
and the perturbation solution becomes
The solution u = u0 + u1 represents eigenmodes in the corresponding 3D structure, which can be computed assuming certain constraints on the axis and possible static prestress and independent of the position along the axis.