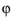
The Solid Mechanics interface, through its equations, describes the motion and deformation of solid objects in a 1-, 2-, or 3-dimensional space. In COMSOL Multiphysics terminology, this physical space is known as the spatial frame, and positions in the physical space are identified by lowercase spatial coordinate variables x, y, and z (or r, , and z in axisymmetric components).

Continuum mechanics theory also makes use of a second set of coordinates, known as material (or reference) coordinates. These are normally denoted by uppercase variables X, Y, and Z (or R, Φ, and Z) and are used to label material particles. Any material particle is uniquely identified by its position in some given initial or reference configuration. As long as the solid stays in this configuration, material and spatial coordinates of every particle coincide and displacements are zero by definition.

More information can be found in About Frames chapter in the COMSOL Multiphysics Reference Manual.

When the solid object deforms due to external or internal forces and constraints, each material particle keeps its material coordinates X (bold font is used to denote coordinate vectors), while its spatial coordinates change with time and applied forces such that it follows a path

in space. Because the material coordinates are constant, the current spatial position is uniquely determined by the displacement vector u, pointing from the reference position to the current position. The global Cartesian components of this displacement vector in the spatial frame, by default called u, v, and w, are the primary dependent variables in the Solid Mechanics interface.

By default, the Solid Mechanics interface uses the calculated displacement and Equation 3-1 to define the difference between spatial coordinates x and material coordinates X. This means the material coordinates relate to the original geometry, while the spatial coordinates are solution dependent.

Material coordinate variables X, Y, and Z must be used in coordinate-dependent expressions that refer to positions in the original geometry, for example, for material properties that are supposed to follow the material during deformation. On the other hand, quantities that have a coordinate dependence in physical space — for example, a spatially varying electromagnetic field acting as a force on the solid — must be described using spatial coordinate variables x, y, and z.