Piezoelectric Losses
Losses in piezoelectric materials can be generated both mechanically and electrically.
In the frequency domain, these can be represented by introducing complex material properties in the elasticity and permittivity matrices. Taking the mechanical case as an example, this introduces a phase lag between the stress and the strain, which corresponds to a Hysteretic Loss. These losses can be added to the Piezoelectric Material by three subnodes: Mechanical Damping, Coupling Loss, and Dielectric Loss. The losses typically defined as loss factors (see below).
The hysteretic electrical losses are usually used to represent high frequency electrical losses that occur as a result of friction impeding the rotation of the microscopic dipoles that produce the material permittivity.
Low frequency losses, corresponding to a finite material conductivity, can be added to the model through an Electrical Conductivity (Time Harmonic) subnode. This feature operates only in the frequency domain.
In the time domain, the losses can be added by:
•
Using the Rayleigh Damping option in the Mechanical Damping and Coupling Loss subnodes to the Piezoelectric Material,.
Rayleigh Damping
•
Using either the Dispersion, or Complex permittivity, or Maximum Loss Tangent option in the Dielectric Loss subnode to the Piezoelectric Material.
These types of damping are also available in the frequency domain.
Rayleigh Damping
Hysteretic Loss
In the frequency domain, the dissipative behavior of the material can be modeled using complex-valued material properties, irrespective of the loss mechanism. Such hysteretic losses can be applied to model both electrical and mechanical losses. For more information about hysteretic losses, see Ref. 1 to Ref. 4.
For the case of piezoelectric materials, this means that the constitutive equations are written as follows.
For the stress-charge formulation
where T is the stress tensor, and S is the strain tensor.
For the strain-charge formulation,
All constitutive matrices in the above equation can be complex-valued matrices, where the imaginary parts define the dissipative function of the material.
Both the real and complex parts of the material data must be defined so as to respect the symmetry properties of the material being modeled and with restrictions imposed by the laws of physics.
A key requirement is that the dissipation density is positive; that is, there is no power gain from the passive material. This requirement sets rules for the relative magnitudes for all material parameters. This is important when defining the coupling losses.
In COMSOL, you can enter the complex-valued data directly or by means of loss factors. When loss factors are used, the complex data is represented as pairs of a real-valued parameter
and a loss factor
the ratio of the imaginary and real part, and the complex data is then:
where the sign depends on the material property used. The loss factors are specific to the material property, and thus they are named according to the property they refer to, for example, ηcE. For a structural material without coupling, simply use ηs, the structural loss factor.
The loss factors are defined so that a positive loss factor value usually corresponds to a positive loss. The complex-valued data is then based on sign rules.
By default, there is no damping until at least one of the damping and losses related subnodes is added.
For the Piezoelectric Material node, the following equations apply via the corresponding three subnodes:
Mechanical Damping
where m and n refer to components of each matrix.
Coupling Loss
Dielectric Loss
Note that the multiplication is applied component-wise.
The loss factors can also be entered as scalar isotropic factors independently of the material and the other coefficients.
A good check on the chosen values is to compute a number of eigenfrequencies, possibly using some different sets of boundary conditions. All computed eigenfrequencies must have a positive imaginary part in order to represent a damped motion.
In practice, it is often difficult to find complex-valued data for each of the matrix elements in the literature. Measuring the losses independently is a challenging task.
Two important particular cases are available in COMSOL, for which the dielectric loss data can be entered based on experimentally measurable quantities:
•
Complex permittivity
•
Maximum Loss Tangent
Dielectric Dispersion
The Dielectric Loss subnode can be set to use the Dispersion option. In such case, the following equations need to be solved in the time domain:
(2-17)
(2-18)
where you can specify two material parameters: the relaxation time τd and the relative permittivity increment ΔεrS. The latter can be either a matrix or a scalar quantity. This model is a one-term version of the more general Debye dispersion model, Ref. 13.
The constitutive relation is assumed as
(2-19)
where S is the strain tensor, and is the relative permittivity in the high frequency limit (that is, for excitations with a characteristic time much shorter than the relaxation time τd).
The parent Piezoelectric Material node has an input for the relative permittivity, εrS, which is used in stationary study. You can chose how this input will be interpreted in the dispersion computations. The options are:
•
High frequency limit. In such case, will be used.
•
Low frequency limit. In such case, will be used. Note that for consistency, must be always positive valued.
With the absence of free electric charges, Equation 2-17 and Equation 2-18 can be combined and integrated in time to yield the following equation:
This is the equation form used in COMSOL Multiphysics for time-dependent analysis.
For the eigenfrequency and frequency domain analyses, the corresponding equation is:
In most cases, iω can be factored out, so that the following equation is solved:
This equation, together with the constitutive relation Equation 2-19 gives
(2-20)
where
and
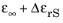
Equation 2-20 shows how the dispersion parameters contribute to the polarization and losses. Thus, the effective relative permittivity decreases with the excitation frequency from the low frequency limit down to the high frequency limit . The damping effect vanishes for both large and small frequencies, and it reaches the maximum for ω = 1/τd.
If your license includes either the AC/DC Module or MEMS Module, more options for modeling dielectric dispersion can be found in Dispersion section in the AC/DC Module User’s Guide.
The following two sections present two cases, for which the dielectric dispersion data can be related to other experimentally measurable quantities. Both cases, can be used in Eigenfrequency, Frequency Domain, and Time Dependent study. The software will apply the dispersion model equations, for which the effective relaxation time and relative permittivity increment are computed automatically based on the node input parameters.
Complex permittivity
In this case, the complex relative permittivity is known at a certain reference frequency
The relaxation time and relative permittivity contribution cane be computed as
where .
If the relative permittivity εrS (input on the Piezoelectric Material parent node) is selected to represent the low frequency limit, one has
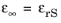
If εrS is selected to represent the high frequency limit, one can simply use instead.
Maximum Loss Tangent
The loss tangent is defined as a function of the frequency
so that the complex relative permittivity can be written as
For many materials, the loss tangent reaches a maximum at certain frequency fref within the frequency range of interested
The relaxation time cane be computed as
where .
If the relative permittivity εrS (input on the Piezoelectric Material parent node) is selected to represent the low frequency limit, the relative permittivity contribution is computes as
where .
If the relative permittivity εrS is selected to represent the high frequency limit, it is computed as
where .
Electrical Conductivity (Time Harmonic)
For frequency domain and eigenfrequency analyses, the effect of electrical conductivity of the piezoelectric material (see Ref. 2, Ref. 5, and Ref. 6) can be included. Thus, in addition to the displacement current, the conduction electric current term is used
where σe is the material electrical conductivity, and E is the electric field. The above form of the equation is used for the eigenfrequency analysis in COMSOL Multiphysics.
When the conduction loss is applied, the default eigenvalue analysis will in most cases return a number of pure imaginary eigenfrequencies. To avoid this, you can configure the solver to search for eigenvalues with real part larger than zero.
Do not use any dielectric loss factor damping together with the conduction loss in an eigenfrequency analysis.
In the COMSOL Multiphysics Reference Manual:
•
Selecting a Stationary, Time-Dependent, or Eigenvalue Solver
•
Eigenvalue Solver
For the frequency domain analysis, the angular frequency is just a parameter, and the equation can be transformed into
which allows you to use both a dielectric loss factor and electrical conductivity in a frequency response study. In such case, ensure that the loss factor refers to the alternating current loss tangent, which dominates at high frequencies, where the effect of ohmic conductivity vanishes (Ref. 7).
Conduction loss can be combined with Dielectric Dispersion for both eigenfrequency and frequency domain analyses. The following equation forms are used, respectively, in the frequency domain:
and in eigenfrequency analyses: