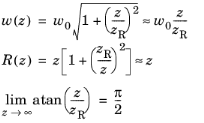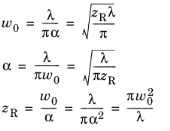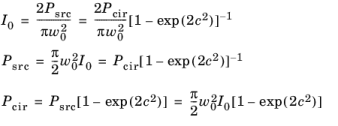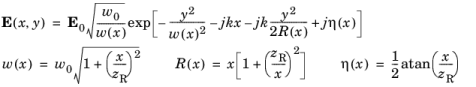You are viewing the documentation for an older COMSOL version. The latest version is
available here.
The Gaussian Beam node releases rays with a Gaussian distribution of intensity or power. It can only be used when solving for either intensity or power, or both.
The Gaussian Beam node is available in 3D, 2D axisymmetric, and 2D geometries. The interpretation of the beam is different in 2D than in 3D or 2D axisymmetric models.
Without loss of generality we assume the beam is propagating in the positive z direction with a waist centered at the origin, although in a 3D geometry any other waist position and beam axis may be specified.
(3-11)
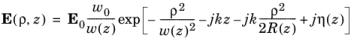
|
•
|
ρ (SI unit: m) is the radial coordinate (with the beam centered around ρ = 0),
|
|
•
|
z (SI unit: m) is the axial coordinate (chosen so that z = 0 is the beam waist),
|
|
•
|
E( ρ, z) (SI unit: V/m) is the electric field at an arbitrary location ( ρ, z),
|
|
•
|
E0 = E(0,0) is the electric field at the center of the beam waist, and
|
|
•
|
k (SI unit: rad/m) is the wave number in the medium through which the beam propagates, k = 2 π/ λ = 2 πn/ λ0 where n (dimensionless) is the absolute refractive index of the medium and λ0 (SI unit: m) is the vacuum wavelength.
|
The beam parameter w0 is called the waist radius. Of course, there is no well-defined cutoff distance at which the electric field goes to zero, so there is a certain degree of arbitrariness involved in assigning a value to the beam radius. As will be shown in the following sections, the beam waist radius is defined such that the fraction of the total beam power that passes through a circle or radius
w0 centered at the origin is 1 -
e-2.
The function w(
z) is the beam radius at any axial coordinate
z,
The function R(
z) describes how quickly the beam phase varies with radial position in a plane located at any axial coordinate
z,
The term η(
z) is an additional phase delay known as the Guoy phase,
In these definitions, zR (SI unit: m) is the Rayleigh range,
The exponent in Equation 3-11 can be separated into amplitude and phase terms,
where δ (SI unit: rad) is the phase factor,
(3-12)
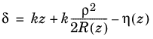
It is also possible to write Equation 3-11 in terms of the irradiance rather than electric field amplitude. As the irradiance
I (SI unit: W/m
2) is proportional to
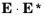
, the phase factor vanishes,
(3-13)
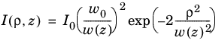
In the asymptotic limit as the z-coordinate is much greater than the Rayleigh range, the beam radius approaches a linear function of
z,
so a beam with radius w(
z) approaches a biconical shape (with both cone vertices meeting at the origin) in the limits
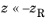
and
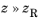
. These asymptotes each make an angle of
α (SI unit: rad) with the beam axis, where
α is called the beam divergence half-angle, to avoid confusion with references such as
Ref. 8 that may define a full angle equal to 2
α.
where r (SI unit: m) is the distance from the origin and
θ (SI unit: rad) is the polar angle measured from the positive
z-axis. Thus
Finally, recall that the Gaussian beam is paraxial (small θ). Taylor series expansions of the cosine and tangent functions reveal that
(3-14)
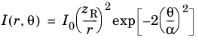
Equation 3-14 shows that the far-field limit of a Gaussian beam (
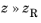
) is a cone of half-angle
α in which the ray intensity or power is proportional to a Gaussian function of the angle between each ray and the beam axis.
The Geometrical Optics interface includes the option to treat rays as fully coherent wavefronts in which the instantaneous phase is solved for, by selecting the Compute phase check box. When the rays are treated as a collimated source, their phase is initialized as if all rays are released at locations along the beam waist. Substituting z = 0 into
Equation 3-12 for the phase factor simply yields
δ = 0, so the initial phase of all released rays is equal.
where L is the maximum distance the rays propagate in the model.
The total power transmitted by the Gaussian beam Psrc (SI unit: m) is found by integrating the irradiance from
Equation 3-13 over a plane perpendicular to the
z-axis,
As expected, the total power crossing a plane perpendicular to the z-axis does not depend on the value of
z, otherwise energy would be accumulating at some location in the beam.
Compare the total source power Psrc with the encircled power
Pcir (SI unit: W/m
2) that passes through a circle of radius
w(
z) centered at the
z-axis,
In addition, by substituting ρ = 0 and
ρ =
w(
z) into
Equation 3-13, it follows that
Thus the beam radius w(
z) is sometimes called the
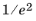
radius. If the above integral is repeated, replacing the upper limit integration with
cw(
z) where
c is a positive constant (called the
Beam cutoff ratio in the settings window), the result is
When the wavelength of the beam λ and any one of the three beam parameters (waist radius
w0, divergence half-angle
α, and Rayleigh range
zR) are defined, the other two beam parameters can be derived:
For a beam of given waist radius w0 and any of the three intensity-related parameters (intensity at the beam waist
I0, total source power
Psrc or encircled power
Pcir), the remaining two parameters can be derived:
Comparing the 2D form with the 3D form from Equation 3-11, the key differences are a square root on the term
w0/
w(x) and a factor of 1/2 in the Guoy phase. In this expression
x has been considered the propagation direction but the beam may actually propagate in any direction in the
xy-plane.
where the error function erf is a built-in function in COMSOL,
For c = 1 the encircled power is about 95% of the total beam power.