The Blackbody Radiation node releases rays diffusely from a surface (following Lambert’s cosine law) with a wavelength or frequency distribution following Planck’s law (if release of polychromatic rays has been enabled) and a total source power based on the Stefan-Boltzmann law (if ray power is solved for).

An ideal blackbody (Ref. 7) is an object that absorbs all radiation that is incident upon it, regardless of the body’s temperature or the wavelength of the radiation.

Real-world objects usually do not behave as ideal blackbody radiation sources. The spectral emissivity ε(λ,T) of an object (dimensionless) is the radiant energy flux per unit surface area the object releases, divided by the radiant energy flux per unit surface area that an ideal blackbody at the same temperature would release. By definition, ε = 1 for an ideal blackbody.

An alternative way to describe the amount of radiation is by using actinometric quantities, which describe the number of photons released rather than the amount of energy. From quantum mechanics, the energy of one photon, the quantum of the electromagnetic field, is defined as E = hν, where ν is the frequency (SI unit: Hz) and h = 6.62607015 × 10-34 J·s is Planck’s constant. Currently the Geometrical Optics interface does not automatically define any variables in actinometric units.

The total radiant exitance 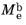(SI unit: W/m2) is the amount of electromagnetic energy emitted from the surface of the blackbody radiation source per unit time, per unit surface area.

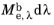
The energy released from a blackbody source follows a wavelength distribution. For some value of the wavelength λ, imagine a sensor that detects 100% of the radiation having wavelengths between λ and λ + dλ, where dλ is an infinitesimally small change in the wavelength, but detects 0% of radiation outside this range. Then the amount of energy detected by this sensor is , where is the spectral radiant exitance. The units of spectral radiant exitance are energy per unit time per unit surface area, per unit wavelength.

The most concise way to write the unit is W/m3 but sometimes it is more conveniently expressed with the area and wavelength units written separately, for example, W/(cm2·μm). The spectral radiant exitance is usually a function of wavelength and temperature, so it may be written as .

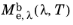
For any two wavelengths λ1 and λ2 (assume λ1 < λ2), the total energy of emitted radiation between these wavelengths is

The spectral radiant exitance may also be written in terms of a spectral quantity other than wavelength, so long as that other quantity has a one-to-one relationship with wavelength. Other quantities that have been used include the frequency, the logarithm of frequency or wavelength, and other powers of frequency or wavelength. In fact there are infinitely many choices for the arbitrarily high powers of λ and ν, of which the first power of wavelength is historically the most common choice (Ref. 7).

The spectral radiance in terms of frequency is written (SI unit: W·s/m2),

The total energy between two wavelengths λ1 and λ2 should be the same when converting these wavelengths to frequencies ν1 = c/λ1 and ν2 = c/λ2,

The order of the limits of integration is reversed because if λ1 < λ2, then ν1 > ν2.

The term cos θ appears in the denominator because the radiance is measured per unit projected surface area from the point of view of an observer at polar angle θ, rather than the actual surface area from which the radiation is emitted.

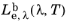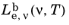
The spectral radiance in terms of wavelength has SI units of W/(m3·sr), or it may be written with the area units and wavelength units separated, for example W/(cm2·nm·sr). Similarly the spectral radiance in terms of frequency has SI units of (W·s)/(m2·sr) but can also be written using different area units.

In general, the spectral radiance may be a function of the polar angle θ. However, the ideal blackbody radiation source is assumed to be a Lambertian source, that is, a diffuse emitter of radiation, meaning the direction distribution of released radiation follows the cosine law. This cosine term exactly cancels out the cosine term appearing in the denominator of Equation 3-8. Therefore the spectral emittance of an ideal blackbody radiation source is independent of the viewing angle.

Although any differential area on the surface of the blackbody releases radiation into the hemispherical half-space above it (subtending a solid angle of 2π steradians), the conversion between exitance and radiance only requires a multiplication by π rather than 2π. This has been shown in the above derivation to follow from the treatment of an ideal blackbody as a Lambertian source.

One might be inclined to substitute λ = c/ν into Equation 3-9 or substitute ν = c/λ into Equation 3-10. Doing so would give seemingly contradictory expressions for the spectral exitance, but doing so would be a mistake because the exitance is not energy flux itself but rather a distribution function of the energy flux (Ref. 7). A better comparison is to integrate Equation 3-9 and Equation 3-10 over matching wavelength and frequency ranges, respectively, noting from Equation 3-7 that these integrals should agree.

To simulate the emission of radiation from a blackbody radiation source, the wavelength or frequency of a representative population of rays must be sampled from the Planck function. To describe how values might be sampled from this distribution function, it is convenient to introduce the dimensionless variable x (not to be confused with the spatial x-coordinate)

It can be shown by taking a series expansion of the integrand and then integrating every term by parts (Ref. 7) that the value of the integral is

where σ is the Stefan-Boltzmann constant,

It is convenient to normalize the spectral exitance so that it represents a probability distribution function of x,

In the COMSOL implementation, when polychromatic radiation is permitted in a model (by selecting either Polychromatic, specify vacuum wavelength or Polychromatic, specify frequency from the physics interface Wavelength distribution of released rays list), values of x are first sampled from the above probability distribution function and then converted to the vacuum wavelength or frequency as needed.