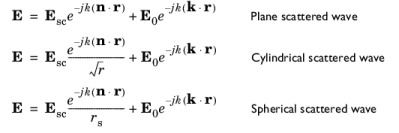Use the Scattering Boundary Condition to make a boundary transparent for a scattered wave. The boundary condition is also transparent for an incoming plane wave. The scattered (outgoing) wave types for which the boundary condition is perfectly transparent are

The field E0 is the incident plane wave that travels in the direction k. The boundary condition is transparent for incoming (but not outgoing) plane waves with any angle of incidence. In addition, to an incident plane wave, E0 can also be the electric field distribution for a Gaussian beam that propagates in the direction k.

If there is an incident field, a Reference Point subnode can be added by right-clicking the context menu (right-click the parent node) or from the Physics toolbar, Attributes menu. The Reference Point subnode redefines the incident field to be expressed as

where rref is a reference point determined by the Reference Point subnode. If no reference point subnode is added, the reference point is calculated as the average position boundary selection.

Select an Incident field — No incident field (the default), Wave given by E field, Wave given by H field, or Gaussian beam. Enter the expressions for the components for the Incident electric field E0 or Incident magnetic field H0.

If the Incident field is set to Gaussian beam, select an Input quantity: Electric field amplitude (the default) or Power. If the Input quantity is Electric field amplitude, enter the component expressions for the Gaussian beam electric field amplitude Eg0 (SI unit: V/m). If the Input quantity is set to Power, enter the Input power (SI unit: W in 2D axisymmetry and 3D and W/m in 2D) and the component expressions for the Gaussian beam non-normalized electric field amplitude Eg0 (SI unit: V/m). Also edit the Beam radius w0 (SI unit: m) and the Distance to focal plane p0 (SI unit: m). The default values are ((10*2)*pi)/emw.k0 and 0 m, respectively. The optical axis for the Gaussian beam is defined by a line including a reference point on the feature selection with a direction specified by the Incident wave direction (see below). By default, the reference point is the average position for the feature selection. However, by adding a Reference Point subnode any available point (or the average of several selected points) on the feature selection can be used as the reference point. The focal plane for the Gaussian beam is located the Distance to focal plane p0 from the reference point in the Incident wave direction.

If the Incident field is not set to No incident field, edit the Incident wave direction kdir for the vector coordinates. The default direction is in the opposite direction to the boundary normal. For 2D axisymmetry, the Incident wave direction kdir should be parallel or anti-parallel to the symmetry axis.

Select a Scattered wave type for which the boundary is absorbing — Plane wave (the default), Spherical wave, or Cylindrical wave.

Expand the Mode Analysis section and check the Subtract propagation constant from material wave number check box to calculate the wave number for the scattered wave as

where kn is the wave number for the scattered wave propagating in the normal direction, k is the material wave number, and β is the propagation constant, determined from the mode analysis. If the check box is cleared (the default), kn = k.

For the Electromagnetic Waves, Transient interface enter the components for the initial value of the Magnetic vector potential A0 (SI unit: Wb/m).

This section is only available for the Electromagnetic Waves, Transient interface. To display it, click the Show More Options button () and select Advanced Physics Options in the Show More Options dialog box.

Select the Dispersion and absorption model that will be used when calculating the wave number and attenuation constant for the incident and scattered waves — Low loss approximation (the default), or High loss. For High loss also enter a Carrier frequency f0 (SI unit: Hz). The default is 1 GHz.