About Richards’ Equation
Richards’ equation models flow in variably saturated porous media. With variably saturated flow, hydraulic properties change as fluids move through the medium, filling some pores and draining others.
This discussion of the Richards’ Equation interface begins with the propagation of a single liquid (oil or water). The pore space not filled with liquid contains an immobile fluid (air) at atmospheric pressure.
Figure 4-1: Fluid retention and permeability functions that vary with pressure head, as given by Van Genuchten formulas available in the Richards’ Equation interface.
Many efforts to simplify and improve the modeling of flow in variably saturated media have produced a number of variants of Richards’ equation since its appearance. The form that COMSOL Multiphysics solves is very general and allows for time-dependent changes in both saturated and unsaturated conditions (see Ref. 1 and Ref. 2):
(4-19)
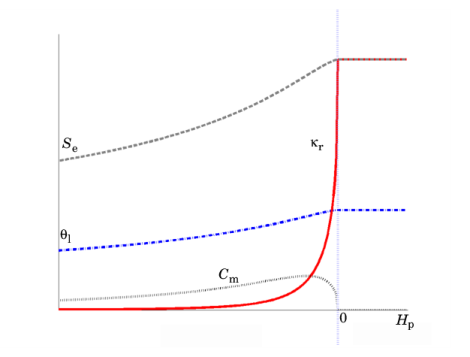
where the pressure, p, is the dependent variable. In this equation, Cm represents the specific moisture capacity, Se denotes the effective saturation, Sp is the storage coefficient, κs gives the hydraulic permeability at saturation, μ is the fluid dynamic viscosity, κr denotes the relative permeability, ρ is the fluid density, g is acceleration of gravity, D represents the elevation, and Qm is the fluid source (positive) or sink (negative).
The fluid velocity across the faces of an infinitesimally small surface is
where u is the velocity vector. The porous medium consists of pore space, fluids, and solids, but only the liquids move. The equation above describes the flux as distributed across a representative surface. To characterize the fluid velocity in the pores, COMSOL Multiphysics also divides u by the liquid volume fraction, θl. This interstitial, pore or average linear velocity is ua = u/θl.