The gravity force is defined from the acceleration of gravity vector, g, and the density, ρ. Under usual conditions and in Cartesian coordinates with the z-axis in the vertical direction,

When gravity is considered, a volume force equal to ρg is included in the momentum equation. For example, for laminar weakly compressible flow, it reads:

Introducing a constant reference density ρref, and assuming that g is homogeneous, this equation is equivalently written:

where r is the position vector and rref is an arbitrary reference position vector.

In Equation 3-32, the gravity force is written .

For incompressible flow the fluid density is assumed to be constant. Hence it is natural to define the reference density, ρref, such that ρ = ρref = ρ (Τref,pref ) which makes it possible to simplify Equation 3-32:

For weakly compressible flow the assumption is that the density depends only on the temperature. In particular, the pressure dependency of the density is neglected, and the density is evaluated at the reference pressure: ρ = ρ(Τ, pref). With the relative pressure as dependent variable, Equation 3-30 is used

With the reduced pressure as dependent variable, Equation 3-32 is used:

For compressible flow the density may depend on any other variable, in particular on the temperature and the pressure. Similar equations are used as for the Weakly Compressible Flow case except that the density is not evaluated at the reference pressure.

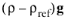
For consistency, when the Nonisothermal Flow coupling is active, the assumptions made for the single phase flow interface are also made in the heat transfer interface:

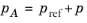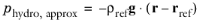
When the relative pressure is used (default option) the interface dependent variable represents the relative pressure and the absolute pressure is defined as . When the pressure is used to define a boundary condition (for example, when p0 defines the pressure condition at an outlet), it represents the relative pressure. Hence defining the outlet pressure as compensates for the gravity force for an ambient reference pressure of 0 Pa when the density is constant, there is no external force, and provided pref, g and r0 are defined consistently.

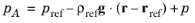
When the reduced pressure is used, the interface dependent variable (named p by default) represents the reduced pressure. The absolute pressure is then defined as . In this case when the pressure is used to define a boundary condition (for example, to define a pressure condition at an outlet), its value corresponds to the reduced pressure. 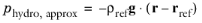Hence, the prescribed pressure compensates for an approximate hydrostatic pressure, which is exact only when the density is constant and there is no external force.
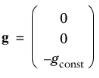