For computing the electron density and electron energy according to Equation 4-5 and Equation 4-6 transport properties and source coefficients are required. These coefficients can be calculated from collision cross-section data and the (unknown) electron energy distribution function (EEDF). The equation formulation used in the physics interface depends on whether the EEDF is an assumed function (Maxwellian, Druyvesteyn or Generalized) or is to be explicitly computed by the Boltzmann equation, using the two-term approximation.

In order to remain consistent with Ref. 1, the unit of electron energy and mean electron energy is specified in volts, rather than electron volts. The two quantities can be converted to each other via the unit charge, which is the built-in variable e_const in COMSOL. So, the mean electron energy (in volts) is equal to the mean electron energy (in units of eV) divided by the unit charge. This makes the equations easier to follow while remaining consistent with the way units are interpreted in COMSOL.

Solving the Boltzmann equation also makes it possible to calculate the drift velocity. The drift velocity is an important quantity because it depends on all the collisions which make up the plasma chemistry. The drift velocity is easy to measure, and comparing the experimental and simulated drift velocity is therefore straightforward. Indeed, collision cross sections are often inferred from drift velocity data.

Verifying that the experimental drift velocity agrees with the computed drift velocity is a good indicator that a given set of cross sections are correct. This physics interface makes it easy to compare the computed drift velocity to experimental data. A treatise on experimental measurements of the drift velocity is available in Ref. 2.

and 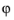is the mean electron energy. Depending on the value of the variable, g, the distribution function is either Maxwellian (g = 1), Druyvesteyn (g = 2), or Generalized (1 < g < 2). Mathematically, the distribution functions are defined as: