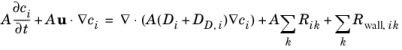The Transport of Diluted Species in Pipes Interface theory is described in this section. This physics interface solves a mass balance equation for pipes in order to compute the concentration distribution of a solute in a dilute solution, taking the flow velocity as input.
where A (SI unit: m2) is the cross section area available for flow,
ci (SI unit: mol/m
3) is the diluted species concentration, and
u a velocity field. Further,
Di (SI unit: m
2/s) is the species diffusion coefficient and
DD,i (SI unit: m
2/s) is the species dispersion coefficient. The second term on the right hand side,
Rik (SI unit: mol/(m
3·s)), corresponds a source or sink due to chemical reaction number
k for species
i. Finally,
Rwall,ik (SI unit: mol/(m·s)), is a source term due to mass transfer contribution
k through the pipe wall.
For laminar flow in circular straight pipes, the total dispersion is given by the sum of molecular diffusion, Di (SI unit: m
2/s), and the effect of the velocity profile causing some fractions of an initial plane of fluid in the pipe to move faster than others. COMSOL Multiphysics
uses the Taylor (
Ref. 22) correlation for this second contribution,
DD,i (SI unit: m
2/s):
where d is the pipe diameter and
L a characteristic pipe length. For turbulent conditions, Taylor (
Ref. 23) suggests:
with k for Power-law fluids given by:
and k for Bingham plastic fluids:
where R is the pipe radius and
r0 is the radius of the plug flow region in the plastic flow, defined as