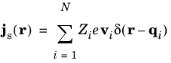Current Density Calculation
Given an array of idealized point sources such that the position vector of the ith source is denoted qi (SI unit: m), the contribution to the current density by particles js at position r is
(6-11)
where
•
δ is the Dirac delta function,
•
Zi (dimensionless) is the charge number of the ith particle,
•
e = 1.602176634 × 10-19 C is the elementary charge,
•
vi (SI unit: m/s) is the velocity of the ith particle, and
•
N (dimensionless) is the total number of particles.
The equation for the current density is unusable in this form, however, because the number of particles involved may be extraordinarily large, and because the transfer of information from the point particles to degrees of freedom defined on a finite element mesh introduces some discretization error. In the following sections we discuss solutions to these problems.
Modeling a Representative Sample of Particles
Because the number of real particles, such as ions or electrons, may be too large for every particle to be modeled individually, a practical numerical approach is to release a representative sample of model particles, allowing each model particle to make the same contribution to the current density as an equivalent number of real particles.
For example, instead of allocating degrees of freedom for 1012 electrons, it will often suffice to model 104 particles, each of which has a Charge multiplication factor of 108, meaning that it represents 108 electrons.
Simplification for Constant-Current Beams
If a beam of particles is released at constant current, then a full time-domain calculation of the coupled particle trajectories and electric and magnetic fields may require particles to be released at a large number of time steps until a stationary solution for the electric potential and magnetic vector potential is reached. This can be needlessly memory-intensive and time-consuming. An alternative approach is to release particles at time t = 0 and to allow each model particle to represent a continuous stream of real particles per unit time. The number of real particles per unit time represented by each model particle is denoted the effective frequency of release, frel.
The charged particles will contribute to the current density along their entire trajectories, not just at their instantaneous positions. This behavior can be conveniently reproduced by defining an expression for the time derivative of the current density, rather than the current density itself:
(6-12)
The current density can then be computed by integrating over time, as long as sufficient time is given so that the particle trajectories can be traced completely through the modeling domain.
The frequency of release can be computed using the current and number of model particles that are specified in release feature settings. For example, for an Inlet node with release current magnitude I (SI unit: A) and number of particles per release N (dimensionless), the effective frequency of release is
When particle beams are assumed to have constant current, then the current density at the last time step includes contributions from particles at every point along their trajectories in the modeling domain. Thus, it can be applied as the current density term when computing the magnetic vector potential.
The treatment of particle beams as constant-current beams is determined by the Particle release specification list in the settings window for the Charged Particle Tracing physics interface. If Specify release times is selected, the charge density is computed using Equation 6-11 and is determined by the instantaneous positions of all model particles. Thus, it is necessary to solve for the particle trajectories, electric potential, and magnetic vector potential in the time domain. If Specify current is selected, the current density is computed using Equation 6-12 and is determined by the time history of the model particle positions.
The difference between the Specify current and Specify release times particle release specifications is thus analogous to the difference between integration over Elements and time and integration over Elements as described for the Accumulator (Domain) node.
At this point, the effect of a bidirectional coupling between the particle trajectories and fields has not been considered. If Specify release times is selected from the Particle release specification list, this does not require special consideration because the trajectories and fields are computed simultaneously. If Specify current is selected, however, the trajectories and fields are computed using different study types, and an additional feedback mechanism is needed. The Bidirectionally Coupled Particle Tracing study step generates a solver sequence that does the following:
1
Set the current density contribution due to the particles to zero.
2
Compute the magnetic vector potential and other field variables using a Stationary solver, using the value of the current density computed in the previous step.
3
Compute the particle trajectories and the resulting current density in the time domain, using the field variables computed in the previous step.
4
Repeat steps 2 and 3 until a specified number of iterations has been reached, or until another user-specified convergence criterion has been satisfied.
Given a sufficient number of iterations, the resulting solution will fully account for the bidirectional coupling between the particle trajectories and stationary fields.
Avoiding Infinitely Large Values of the Current Density
The Magnetic Particle Field Interaction node defines a variable for each component of the contribution to the current density by particles in each mesh element. This variable is discretized using constant shape functions. For a mesh element j with volume Vj, and with the Particle release specification set to Specify release times, the average current density ρj is
where ni (dimensionless) is the charge multiplication factor of the ith model particle. The integral on the right-hand side is a volume integral over element j. The resulting current density is the average current density over the mesh element, which may be written as
where the sum is taken over all particles that are within mesh element j.
If instead the Particle release specification is Specify current, each model particle represents a number of particles per unit time which follow along the same path, determined by the effective frequency of release frel. Then the time derivative of the current density can be expressed as