The formulation of the equations of motion is specified by selecting an option from the Formulation list in the physics interface Particle Release and Propagation section. The available options for each physics interface are listed in Table 2-1.

Choosing an appropriate formulation can help to reduce computational cost or improve accuracy. For example, when tracing macroscopic particles in a fluid, the inertia of particles may be extremely important or negligible, depending on the size of the particles; so the modeling process often begins with the fundamental choice of whether to use the Newtonian or Newtonian, ignore inertial terms formulation.

The Newtonian formulation is the default and the most common formulation. It defines a set of second-order ordinary differential equations for the components of the particle position based on Newton’s second law of motion,

where q (SI unit: m) is the particle position, mp (SI unit: kg) is the particle mass, and F (SI unit: N) is the total force on the particles.

The Newtonian, first order formulation is an alternative to the Newtonian formulation. It defines a set of coupled first-order ordinary differential equations for the components of the particle position and velocity,

The default time stepping method for the first-order Newtonian formulation is the Dormand–Prince 5 Runge–Kutta method, an explicit time stepping method. By comparison, the second-order Newtonian formulation uses the Generalized alpha implicit method by default.

The explicit time stepping method is less suitable for stiff problems, meaning that the Newtonian formulation is more robust when the particles are subjected to extremely large, abrupt accelerations. The Newtonian formulation is also favorable for problems involving ultrarelativistic particles. However, for some nonstiff problems, the explicit method can give comparable or even better accuracy and performance, compared to the implicit method.

Generally, it is most convenient to begin with the default Newtonian formulation, then to consider switching to the Newtonian, first order formulation to optimize performance if the problem is not overtly stiff.

The Newtonian, ignore inertial terms formulation is only available for The Particle Tracing for Fluid Flow Interface. This formulation is particularly useful for modeling small particles (usually diameters around the micron scale or smaller) in a viscous fluid.

To determine when it is appropriate to use this formulation and when the default Newtonian formulation is preferable, consider the classic example of a spherical particle subjected to Stokes drag. Neglecting gravity, the equation of motion of this particle is

where ρp (SI unit: kg/m3) is the density, the equation of motion can also be written as

where τp (SI unit: s) is the particle velocity response time (sometimes called the characteristic time or the Lagrangian time scale),

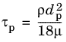
If the fluid velocity u is spatially uniform, then the difference between the particle velocity and fluid velocity decays exponentially with time scale τp,

The velocity time scale τp defined in Equation 2-1 indicates how quickly a particle accelerates when its velocity is different than the velocity of the surrounding fluid.

For a particle with density 1800 kg/m3, diameter 1 μm, and a fluid of dynamic viscosity 1 m·Pa·s, the time scale is 0.1 μs, or one ten-millionth of a second. Most time stepping algorithms are not unconditionally stable and can produce nonphysical oscillations in particle position if the time step is too large. If the total duration of the Time Dependent study is on the order of one second, then such a study could potentially require millions of time steps to accurately resolve the acceleration of particles in the fluid, especially if the fluid velocity is not spatially uniform.

The Newtonian, ignore inertial terms formulation simplifies the motion of the particle by assuming that it reaches a dynamic equilibrium with the velocity of the surrounding fluid instantaneously. That is, instead of solving an equation of the form

In conclusion, the Newtonian, ignore inertial terms formulation is a simplified set of first-order equations for the particle position. It should be used when the particle inertia does not play a significant role in the simulation. This is most often true when the particle velocity response time is extremely small compared to the duration of the transient study.

The Massless formulation defines a set of first-order ordinary differential equations for the components of the particle position only. The particle velocity is directly specified, either by an expression or by using a previously computed field.

The Massless formulation is useful for tracing particles along streamlines. These may be fluid velocity streamlines, electric field lines, or based on some other expression. A useful technique for integrating along streamlines is to use a particle tracing interface with the Massless formulation, then define one or more Auxiliary Dependent Variable nodes, specifying the expressions to be integrated over time or along the trajectories.

The Lagrangian formulation (Ref. 2, Chapter 1) defines a set of second-order ordinary differential equations for the components of the particle position. Compared to the Newtonian formulation, the Lagrangian formulation has the same number of degrees of freedom and offers greater flexibility in specifying the equations of motion, but it is not possible to use the Force feature.

The equation of motion for a system with Lagrangian L (SI unit: J) is

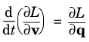
where v (SI unit: m/s) is the particle velocity and q (SI unit: m) is the particle position. Equation 2-2 is called the Euler-Lagrange equation.

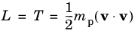
For example, for an instance of The Mathematical Particle Tracing Interface with tag pt in 3D, the expression pt.mp*(pt.vx^2+pt.vy^2+pt.vz^2)/2 is the Lagrangian for a free particle that is not subjected to any forces. Note that substitution into the Euler-Lagrange equation yields

where T (SI unit: J) is the particle kinetic energy and U (SI unit: J) is the total potential energy. For example, if U only depends on particle position, not velocity, then substitution into the Euler-Lagrange equation yields

The Hamiltonian formulation defines a set of coupled first-order ordinary differential equations for the components of the particle position and generalized momentum.

Following Chapter 7 in Ref. 2 the Hamiltonian H (SI unit: J) can be derived directly from an expression for the Lagrangian L. The degrees of freedom are the position vector components qi and the generalized momenta pi, defined as

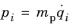
for i from 1 to the total number of space dimensions. Thus, in this case the generalized momentum is simply the particle momentum.

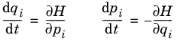
These are known as Hamilton’s equations.

Substitution with Equation 2-3 and Equation 2-4 then yields

Since the default name for The Mathematical Particle Tracing Interface is pt, the Hamiltonian of a free particle in 3D would then be (px^2+py^2+pz^2)/(2*pt.mp). Substitution into Hamilton’s Equations then yields