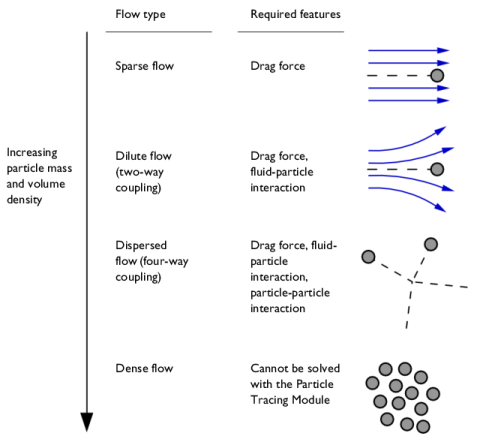
The Particle Tracing for Fluid Flow Interface is designed for modeling microscopic and macroscopic particles in a background fluid. There are two phases in the system: a particle phase consisting of discrete bubbles, particles, droplets, and so forth; and a continuous phase in which the particles are immersed. In order for the particle tracing approach to be valid, the fluid system should be a
dilute or
dispersed flow. This means that the volume fraction of the particles is much smaller than the volume fraction of the continuous phase, generally less than
1%. When the volume fraction of the particles is not small, the fluid system is categorized as a
dense flow and a different modeling approach is required.
In the physics interface Particle Release and Propagation section, choose one of the following options from the
Formulation list:
When using the Newtonian formulation or the
Newtonian, first order formulation, the maximum time step taken by the solver is determined by the smallest particles in the flow. The time-step size to fully resolve particle acceleration in the flow is proportional to the square of the particle diameter, so reducing the particle diameter by ten means that 100 times as many time steps are needed to accurately resolve the particle motion.
In a sparse flow, the continuous phase affects the motion of the particles, but the volume force exerted on the fluid by the particles is deemed insignificant. This is often referred to as a unidirectional coupling. Often the fluid velocity field can first be computed using a separate physics interface, such as the Laminar Flow interface. Then this velocity field can be used to define the drag force on the particles (via the
Drag Force node). The fluid velocity can be stationary or time-dependent, whereas the particle trajectories are always computed in the time domain.
The body force exerted on the fluid by the particle is applied in an approximate way, in that it is smeared out over a mesh element. This smearing effect makes the volume force computed by the Fluid-Particle Interaction node somewhat mesh dependent. When modeling fluid-particle interactions for which the mass flow rate of particles is not constant, the continuous phase and dispersed phase must be computed simultaneously in the same study. The computational demand is significantly higher than in the
Sparse Flow case.
If the fields are stationary, as often occurs when particles are released at constant mass flow rate, it may be possible to compute the particle trajectories using a Time-Dependent solver while computing the fluid flow variables using a
Stationary solver. It is also possible to create a solver loop that alternates between the
Stationary and
Time-Dependent solvers so that a bidirectional coupling between the trajectories and fields can be established; a dedicated
Bidirectionally Coupled Particle Tracing study step is available for setting up such a solver loop. The process of combining these solvers is described in the section
Study Setup.
Built-in auxiliary dependent variables for the mass and temperature can be activated by selecting the Compute particle mass and
Compute particle temperature check boxes, respectively, in the
Additional Variables section of the Settings window for the physics interface. When the option to compute particle mass is activated, it is possible to set the initial particle mass in particle release features, such as
Release,
Inlet, and
Release from Grid. It is also possible to select a distribution function for the initial mass or diameter. This is important when modeling separation devices where the goal is to understand the
transmission probability of particles of various sizes.
The Brownian Force is most significant when the particles are extremely small, generally in the submicron range. Brownian motion causes particles to drift because the number of molecules striking each particle from different sides is random, since the molecules in a fluid (even at room temperature) move around randomly and at high speeds. When the particles are larger, Brownian motion is less of a driving factor because the number of molecules hitting the particle surface is large enough that they tend to average out more readily.
Turbulent dispersion can be enabled in the settings for the Drag Force. The fluid surrounding the particles can become turbulent when its Reynolds number becomes sufficiently large. Turbulence is generally associated with faster fluid velocity, larger geometric length scale, and lower viscosity. In a turbulent flow, the fluid velocity field includes a large number of swirls or eddies that rapidly change direction.
To compute particle trajectories in a turbulent flow, in the settings for the Drag Force you can select
Discrete random walk or
Continuous random walk from the
Turbulent dispersion model list. To compute the drag force, then, the fluid velocity encountered by each particle is treated as the sum of the mean flow term and a random perturbation term.
Many drag laws that are available in the Drag Force node, such as the Stokes drag law, are based on the assumption of continuum flow, in which the particle Knudsen number
Kn (dimensionless) is very small,
where λ (SI unit: m) is the mean free path of molecules in the surrounding fluid, and
L (SI unit: m) is a characteristic length of the particle, such as the particle diameter. The exact definition of the characteristic length may vary depending on the source being cited and should be considered with caution.
When the particles are extremely small or they are surrounded by a rarefied gas, the assumption of continuum flow may not be valid. By selecting the Include rarefaction effects check box in the physics interface
Particle Release and Propagation section, it is possible to apply correction factors to the
Drag Force and
Thermophoretic Force, enabling accurate modeling of particle motion in the slip flow, transitional flow, and free molecular flow regimes.