About the Boundary Conditions for the Particle Tracing Interfaces
The equations of motion for the particle trajectories are supplemented with a variety of options to describe how the particles behave when they contact surfaces in the geometry.
About the Wall Boundary Conditions
The following nomenclature is used with time as an example:
•
Value of a variable precontact, w.
•
Value of a variable at the moment of contact, wc.
•
Value of a variable postcontact, w'.
When a particle comes in contact with a wall, at time tc, the following options are available for what happens as a result of the particle-wall interaction.
Disappear
When the particle strikes the wall it disappears from view. Mathematically the particle location is set to not-a-number (NaN) at all time steps after the particle makes contact with the wall:
This condition means that the particle is not rendered during results processing.
Freeze
The particle position and velocity remain the same at all time steps t > tc:
Because the velocity is frozen at the time of impact, this boundary condition allows for recovery of velocity and energy distribution functions.
Stick
The particle follows the motion of the wall after contact:
Bounce
The particle is reflected from the wall in the tangent plane. The incident angle and reflected angle are the same with respect to the surface normal:
This conserves energy if the Hamiltonian depends isotropically on momentum.
Diffuse and Isotropic Scattering
The particle is reflected from the wall with a pseudorandomly generated velocity vector. Specifically, for the particle position:
and for the particle velocity in 3D:
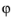
where θ is the polar angle and is the azimuthal angle. For both diffuse and isotropic scattering, the azimuthal angle is uniformly distributed in the interval [0, 2π].
For diffuse scattering, the probability distribution function of the polar angle follows the cosine law, which states (Ref. 2) that the flux dn of reflected particles within a differential solid angle dω is proportional to the cosine of the polar angle,
and noting that the differential solid angle is
the probability distribution function of azimuthal and polar angles within a hemisphere about the surface normal n is
A value of the polar angle can be sampled from this distribution function by first defining a uniform random number Γ between 0 and 1. Then the polar angle is
For isotropic scattering, the flux of reflected particles is the same for any differential solid angle dω; the flux is not proportional to cos θ. The probability distribution function is
Again defining a uniform random number Γ between 0 and 1, the polar angle is now
In 2D, the tangential and normal velocity components are:
where for diffuse scattering the angle θ is defined as:
or for isotropic scattering,
where Γ is uniformly distributed within the given interval.
Mixed Diffuse and Specular Reflection
The particle has probability γ to be reflected specularly, as if using the Bounce condition. Otherwise the particle is reflected diffusely, as if using the Diffuse scattering condition.
General Reflection
The general reflection option allows for arbitrary velocities to be specified for the particles after they strike the wall:
and
where vp (SI unit: m/s) is the user-defined velocity vector. The velocity can be specified either in Cartesian coordinates or in the normal-tangent coordinate system.
About the Inlet Boundary Conditions
At the inlet the number of particles, particle position, initial velocity, and the number of releases is specified. An Inlet node can contribute with a Wall or Outlet node, so it is possible to specify a behavior for particles that return to the inlet at a later time.
About the Outlet Boundary Conditions
At the outlets the particles either freeze or disappear.
Thermal Re-Emission
At a boundary with the Thermal Re-Emission feature, particles are reflected into the modeling domain as if they were adsorbed at the wall and re-emitted with the wall temperature.
The reflected particle speed is sampled from a distribution based on space dimension:
where
•
W (dimensionless) is the normalized kinetic energy,
•
V (SI unit: m/s) is the speed of the reflected particle,
•
T (SI unit: K) is the wall temperature,
•
mp (SI unit: kg) is the particle mass, and
•
kB = 1.380649 × 10-23 J/K is the Boltzmann constant.
The 3D form of f(W) is used in 3D models and in 2D models where the Include out-of-plane degrees of freedom check box has been selected.
The values of W for 2D and 3D are gamma(1.5,1) and gamma(2,1) distributed random variables, respectively. The generators used to sample values of W are (Ref. 3)
Where N is a normally distributed random number with zero mean and unit variance, and the Ui are uncorrelated uniformly distributed random numbers between 0 and 1.
The distribution of reflected particle directions follows Knudsen’s cosine law; it is the same direction distribution as the Diffuse scattering condition for the Wall feature.