Thermionic Emission Theory
The Thermionic Emission feature is used to release electrons from a hot cathode. It releases model particles from a boundary such that the emitted current density magnitude Jth (SI unit: A/m2) is (Ref. 12)
where
•
T (SI unit: K) is the temperature of the cathode,
•
Φ (SI unit: V) is the work function of the metal,
•
A∗ (SI unit: A/(m2·K2)) is the effective Richardson constant,
•
kB = 1.380649 × 10-23 J/K is the Boltzmann constant, and
•
e = 1.602176634 × 10-19 C is the elementary charge.
The total current Ith (SI unit: A) released from the surface is
where the surface integral is taken over the selected boundaries.
Initial Velocity Directions
The initial particle velocity components are
where vn is the velocity component normal to the cathode surface and vt1 and vt2 are the two orthogonal velocity components parallel to the surface. The azimuthal angle  is uniformly distributed in the interval [0, 2π]. The polar angle θ is
where U1 is a uniformly distributed random number in the interval [0, 1]. The particle speed V (SI unit: m/s) can be sampled from a probability distribution function in several different ways, which are described in the following section.
Initial Speed
The probability distribution function of the initial electron speed is more easily expressed in terms of the normalized kinetic energy W (dimensionless), defined as
(4-13)
where me = 9.10938356 × 10-31 kg is the electron mass. The thermal electrons are assumed to be nonrelativistic. The probability distribution function of the normalized kinetic energy is
(4-14)
The way in which the initial particle kinetic energy is sampled from this probability distribution function is controlled by the Weighting of macroparticles list in the physics feature Initial Velocity section.
Uniform Current
For Uniform Current the values of the normalized kinetic energy for the particles are pseudorandom numbers sampled directly from Equation 4-14. The generator used to sample values of W is (Ref. 13)
Where U1 and U2 are uncorrelated uniformly distributed random numbers in (0,1).
Because the initial particle energy is sampled from the probability distribution function given in Equation 4-14, each particle carries the same weight; that is, each model particle is a macroparticle representing an equal number of electrons emitted per unit time. This macroparticle weighting is represented by a static degree of freedom stored for all model particles called the effective frequency of release frel,
To yield the specified total current Ith, the effective frequency of release of the ith model particle must be
where N (dimensionless) is the total number of model particles released by the feature.
For more information on the effective frequency of release and its effect on space charge density calculation, see Space Charge Density Calculation in Theory for the Particle Field Interaction, Non-Relativistic Interface.
Uniform Energy Intervals
When Uniform energy intervals is selected, the initial normalized kinetic energy of each particle is uniformly sampled from the interval [0, n], where n is a user-defined proportionality factor. Because the energy is uniformly sampled instead of following the probability distribution given by Equation 4-14, the probability distribution must instead be incorporated into the effective frequency of release:
(4-15)
Thus the effective frequency of release of the ith particle is
where the sum over j in the denominator is taken over all model particles released by the feature.
Equation 4-14 has a local maximum at W = 1, after which it gradually decreases. Some representative values of the CDF are given in Table 4-5.
Table 4-5: Selected Values of the CDF for Normalized Electron Energy
W
CDF
3.89
0.9
6.64
0.99
9.23
0.999
Therefore a value of n = 10, for example, will encompass more than 99.9% of the cumulative distribution function.
Uniform Speed Intervals
When Uniform speed intervals is selected, the initial speed of each particle is uniformly sampled from the interval [0, Vmax], where
where n (dimensionless) is a user-defined proportionality factor.
Differentiating both sides of Equation 4-13 and rearranging yields
Substituting into Equation 4-14 yields
Therefore, compared to Equation 4-15 the proportionality factor is multiplied by an additional term proportional to :
(4-16)
Thus the frequency of release of the ith particle is
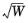
where again the sum over j in the denominator is taken over all model particle emitted by the feature.
When to Sample from Uniform Energy or Speed Intervals
The main motivation for selecting Uniform energy intervals or Uniform speed intervals is that these options devote a disproportionately large number of degrees of freedom to electrons at the extreme ends of the probability distribution function. For example, when sampling from Uniform energy intervals with n > 8, equal representation would be given to particles in the neighborhood of W = 1 and W = 7.64, despite W = 1 having a probability density 100 times more greater than W = 7.64.
It can be useful to devote additional degrees of freedom to particles with extremely high and low energy because these particles may have a greater influence on the behavior of a system than electrons of the most probable energy, and therefore they might require finer discretization in velocity space to yield a statistically converged solution. For example, in plane parallel vacuum diodes in the space charge limited regime, the presence of electrons between the electrodes creates a potential barrier which only the most energetic electrons can bypass. Devoting more degrees of freedom to the most energetic electrons in the distribution, despite the low percentage of the overall number of electrons that they represent, can lead to a more robust and reproducible solution because a larger sample of model particles is used to compute the charge density in the region beyond the potential barrier.