You are viewing the documentation for an older COMSOL version. The latest version is
available here.
|
|
The Magnetic Force node is only available when Newtonian or Newtonian, first order is selected as the Formulation in the physics interface Particle Release and Propagation section
|
Use the Magnetic Force node to define the magnetic component of the Lorentz force. This causes the particle to curve perpendicularly to the particle velocity and magnetic field. A magnetic force alone does no work on the particles, so in the absence of any other external forces, the particle retains its original energy. Some small variation in the particle kinetic energy can be expected, but it is just due to numerical error and can usually be reduced by adjusting the solver settings. The force is specified via a magnetic flux density.
Enter values or expressions in the table for the Magnetic flux density B (SI unit: T) based on space dimension, or, if the magnetic flux density is computed by another physics interface, select another option from the list.
|
|
With the AC/DC Module see Magnetic Lens: Application Library path Particle_Tracing_Module/Charged_Particle_Tracing/magnetic_lens.
|
Select Earth’s magnetic field from the
Magnetic flux density list to use measurements of Earth’s magnetic field to compute the magnetic force. The external data is from the International Geomagnetic Reference Field (IGRF;
Ref. 2). Select an option from the
Location specification list:
From particle positions (default) or
Geographic location. Enter a value or expression for the
Epoch E (dimensionless) to determine which measurements are used to compute Earth’s magnetic field. The default value is 2015. The IGRF data is tabulated in 5-year increments, and data from 1950 to 2015 is included for the
Magnetic Force node.
If From particle positions is selected, the magnetic force is computed by treating the particle coordinates as position vector components with respect to the center of Earth, such that the geographic North pole points in the positive
z direction and the Prime Meridian intersects the positive
x-axis.
If Geographic location is selected the magnetic field components are assigned constant values based on the specified location. This is appropriate when the modeling domain is very small relative to the length scales over which Earth’s magnetic field changes significantly. By default, the magnetic field is determined based on the assumption that the positive
x-axis points to the North, the positive
y-axis points to the West, and the positive
z-axis points upward. Select an option from the
Location defined by list:
City (the default) or
Coordinates. If
City is selected, choose one of several major cities available in the
City list. The default is
Las Vegas, USA. If
Coordinates is selected, enter the
Latitude Φ and
Longitude Θ. Positive values indicate latitude North of the equator and longitude East of the Prime Meridian, respectively. The default values are
36.1°N,
115.2°W.
|
|
For the Latitude and Longitude it is important to indicate that the entered quantities are in degrees, usually by including [deg] after the numeric value. Otherwise, numeric values with no specified unit will be interpreted in the default plane angle unit, which is typically the radian.
|
For both options in the Location defined by list, enter the
Altitude h (SI unit: m). The default is
0.
Select an option from the Time dependence of field list:
Stationary or time dependent (the default),
Time harmonic, or
Periodic.
The default, Stationary or time dependent, does not modify the magnetic flux density when computing the force on the particles. This is appropriate for any of the following cases:
Select Time harmonic when the field was computed using a Frequency Domain or Eigenfrequency study. The field is multiplied by a sinusoidal phase factor,
where B (SI unit: T) is the magnetic flux density used to compute the force,

(SI unit: T) is the complex-valued magnetic flux density computed in the previous study, and
ω (SI unit: rad/s) is the angular frequency. The angular frequency can be taken directly from the previous Frequency Domain or Eigenfrequency study, or it can be specified directly or in terms of the period.
Select Periodic when the field was computed using a previous Time Dependent study but is assumed to repeat over subsequent time intervals. This allows the trajectories of charged particles to be computed over many periods, while only having to solve for the magnetic flux density over a single period. The field is assumed to be periodic but is not required to oscillate sinusoidally over time; in this sense, the
Periodic option is a generalization of the
Time harmonic option.
where t (SI unit: s) is the time,
Δt (SI unit: s) is a user-defined time delay, and
T (SI unit: s) is the period. Here
mod is the modulo operator, which adds or subtracts a multiple of
T from the first argument such that its value is between
0 and
T.
For Time harmonic or
Periodic, select an option from the
Frequency specification list:
From solution (the default),
Specify frequency, or
Specify period. For
Specify frequency, enter the
Angular frequency ω (SI unit: rad/s). The default is
1 MHz. For
Specify period, enter the
Period T (SI unit: s). The default is
1 μs.
For Time harmonic, also specify the
Initial phase angle 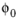
(SI unit: rad). The default is
0.
For Periodic, also enter the
Time shift Δt (SI unit: s). The default is
0.
Select the Use piecewise polynomial recovery on field check box to smooth the magnetic flux density using piecewise polynomial recovery. This can give a much more accurate representation of the magnetic flux density as it uses information on adjacent mesh elements to reconstruct the field. If a coarse mesh is used to compute the field then this option can be especially useful.
Use the Particles to affect list to apply the force to specific particles. The available settings are the same as for the
Force node.