
|
|
•
|
|
•
|
|
•
|
|
•
|
|
•
|
|
1
|
|
2
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
1
|
|
2
|
|
4
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material.
|
|
2
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
Click the Custom button.
|
|
4
|
|
1
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
9
|
|
1
|
|
1
|
|
3
|
|
4
|
|
1
|
|
3
|
|
4
|
|
1
|
|
3
|
|
4
|
From the list, choose Diagonal.
|
|
5
|
|
1
|
|
2
|
|
3
|
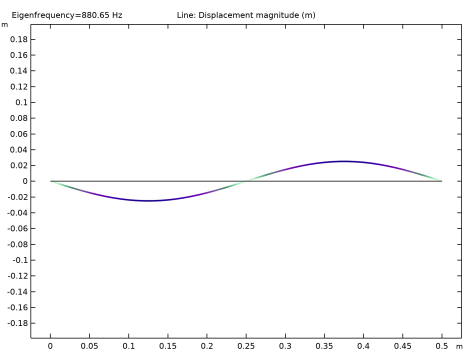
Find the Studies subsection. In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Eigenfrequency, Prestressed.
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
In the tree, select Component 1 (comp1)>Wire (wire)>Elastic Wire 1>Initial Stress and Strain 1 and Component 1 (comp1)>Wire (wire)>Pinned 1.
|
|
4
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
In the tree, select Component 1 (comp1)>Wire (wire)>Elastic Wire 1>Initial Stress and Strain 1, Component 1 (comp1)>Wire (wire)>Pinned 1, and Component 1 (comp1)>Wire (wire)>Spring Foundation 1.
|
|
5
|
Click
|
|
6
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
In the tree, select Component 1 (comp1)>Wire (wire)>Pinned 2, Component 1 (comp1)>Wire (wire)>Prescribed Displacement 1, Component 1 (comp1)>Wire (wire)>Point Load 1, and Component 1 (comp1)>Wire (wire)>Spring Foundation 1.
|
|
5
|
Click
|