PDF
Wi-Fi Booster Yagi–Uda Antenna
Introduction
The 2.4 GHz band outperforms the 5 GHz band when it comes to Wi-Fi coverage. This is because the 2.4 GHz band corresponds to longer wavelengths that can more easily penetrate solid objects, meaning the signal can be better carried out throughout home. On the other hand, eavesdropping is more likely to occur for the personal network. In this model, a Yagi–Uda antenna is designed as shown in Figure 1 for the 2.4−2.5 GHz band. This antenna can direct the signal in a particular direction and prevent intruders from eavesdropping on personal Wi-Fi signals. In other words, it could be treated as a “Wi-Fi booster” in the desired direction.
Figure 1: Yagi–Uda antenna along with far-field radiation pattern.
Model Definition
This Yagi–Uda antenna model consists of a cylindrical feeder, a reflector, and four directors. All these elements are placed at an equidistance of 0.2 λ and are supported by a PTFE block. The volumetric region of antenna elements is omitted to simplify the physics setup. This ensures a Perfect Electrical Conductor (PEC) boundary condition is applied by default on all boundaries of the antenna elements. The losses can be accounted for these electrically conducting boundaries by adding an Impedance Boundary Condition (IBC). However, for simplicity, only PEC conditions are considered. The antenna is fed with a user-defined type lumped port having 50 Ω impedance. A Perfectly Matched Layer (PML) domain condition (spherical type) is used as absorbing domain condition. Moreover, the far-field calculation is done at the air-PML domain interfaces.
Firstly, a frequency domain study is carried out for optimized dimensions at a central frequency of 2.45 GHz to analyze the antenna. Later an adaptive frequency-domain study is performed for finer frequency discretization to obtain S-parameter responses in the whole band.
Results and Discussion
The addition of a reflector on the backside can improve the directivity of the isotropically radiating dipole antenna. Further, this can be enhanced by placing directors in front of the feeder and forming a Yagi–Uda antenna. In Figure 2, the electric fields norm is coupled to directors suggesting that the wave is strongly steered by the directors in the +x-axis.
Figure 2: Electric field norm distribution in the antenna E-plane.
The S-parameter response of the antenna is shown in Figure 3. The resonance is occurring at a central 2.45 GHz frequency. The E- and H-plane far-field patterns are shown in Figure 4. In general, E-plane is a plane where the E-field of the antenna is predominantly present and the H-plane is orthogonal to the E-plane. The half-power beamwidth (HPBW) in the E-plane is observed as 58°, which can be further reduced by adding directors at the cost of an increased antenna size. Maximum 10 dBi gain and a front-to-back ratio of 14 dB are obtained. The 3D far-field radiation pattern is also shown in Figure 5.
Figure 3: S-parameter response for Yagi–Uda antenna.
Figure 4: Polar plot: E-plane and H-plane patterns.
Figure 5: 3D Radiation pattern: Far-field gain in dBi.
Notes About the COMSOL Implementation
In this model, the Yagi–Uda antenna is designed at a 2.45 GHz frequency. To analyze the far-field performance of the antenna, a Frequency Domain study is performed at 2.45 GHz.
Then, an Adaptive Frequency Sweep study is carried out to analyze the S-parameter response in the 2.3−2.6 GHz band. The adaptive frequency sweep study has an advantage to reduce computational time for finer frequency discretization. This is achieved by the model order reduction technique and the Asymptotic Waveform Evaluation (AWE) expression. Note that if the AWE expression has a steep gradient, then the simulation is prolonged. Thus the adaptive frequency sweep study is suitable for structures where single resonance or no resonance is expected. Solutions are stored only at port boundaries to reduce the size of the model file size. Otherwise, a finer frequency discretization used in the adaptive frequency sweep would generate a large size of file.
Application Library path: RF_Module/Antennas/yagi_uda_antenna
Modeling Instructions
From the File menu, choose New.
New
In the New window, click  Model Wizard.
Model Wizard
1
In the Model Wizard window, click  3D.
2
In the Select Physics tree, select Radio Frequency>Electromagnetic Waves, Frequency Domain (emw).
3
Click Add.
4
Click  Study.
5
In the Select Study tree, select General Studies>Frequency Domain.
6
Click  Done.
Global Definitions
Parameters 1
1
In the Model Builder window, under Global Definitions click Parameters 1.
2
In the Settings window for Parameters, locate the Parameters section.
3
In the table, enter the following settings:
Name
Expression
Value
Description
f0
2.45[GHz]
2.45E9 Hz
Operating frequency
lda0
c_const/f0
0.12236 m
Operating wavelength
arm_length
0.43*lda0/2
0.026308 m
Dipole antenna arm length
r_antenna
arm_length/20
0.0013154 m
Dipole antenna radius
gap_size
arm_length/100
2.6308E-4 m
Gap between arms
lr
0.48*lda0
0.058735 m
Reflector length
dr
0.2*lda0
0.024473 m
Distance between feeder and reflector
ld
0.35*lda0
0.042827 m
Director length
d
0.2*lda0
0.024473 m
Distance between director
Build a feeder element along with the boundaries for lumped port excitation.
Geometry 1
Cylinder 1 (cyl1)
1
In the Geometry toolbar, click  Cylinder.
2
In the Settings window for Cylinder, locate the Size and Shape section.
3
In the Radius text field, type r_antenna.
4
In the Height text field, type 2*arm_length+gap_size.
5
Locate the Position section. In the z text field, type -(arm_length+gap_size/2).
6
Click to expand the Layers section. In the table, enter the following settings:
Layer name
Thickness (m)
Layer 1
arm_length
7
Clear the Layers on side check box.
8
Select the Layers on bottom check box.
9
Select the Layers on top check box.
Build a reflector element.
Cylinder 2 (cyl2)
1
In the Geometry toolbar, click  Cylinder.
2
In the Settings window for Cylinder, locate the Size and Shape section.
3
In the Radius text field, type r_antenna*1.2.
4
In the Height text field, type lr.
5
Locate the Position section. In the x text field, type -dr.
6
In the z text field, type -lr/2.
Build a director and an array of directors.
Cylinder 3 (cyl3)
1
In the Geometry toolbar, click  Cylinder.
2
In the Settings window for Cylinder, locate the Size and Shape section.
3
In the Radius text field, type r_antenna.
4
In the Height text field, type ld.
5
Locate the Position section. In the x text field, type d.
6
In the z text field, type -ld/2.
7
Click  Build Selected.
Array 1 (arr1)
1
In the Geometry toolbar, click  Transforms and choose Array.
2
Select the object cyl3 only.
3
In the Settings window for Array, locate the Size section.
4
From the Array type list, choose Linear.
5
In the Size text field, type 4.
6
Locate the Displacement section. In the x text field, type d.
7
Click  Build Selected.
8
Click the  Zoom Extents button in the Graphics toolbar.
Build a mechanical supporting structure which holds the feeder, reflector, and directors together.
Block 1 (blk1)
1
In the Geometry toolbar, click  Block.
2
In the Settings window for Block, locate the Size and Shape section.
3
In the Width text field, type 4*d+1*dr+3*r_antenna.
4
In the Depth text field, type r_antenna*3.
5
In the Height text field, type r_antenna*2.
6
Locate the Position section. In the x text field, type -dr-1.5*r_antenna.
7
In the y text field, type -1.5*r_antenna.
8
In the z text field, type -r_antenna.
9
Click  Build Selected.
Move 1 (mov1)
1
In the Geometry toolbar, click  Transforms and choose Move.
2
Click in the Graphics window and then press Ctrl+A to select all objects.
3
In the Settings window for Move, locate the Displacement section.
4
In the x text field, type -(5*d+1*dr+3*r_antenna)/4.
5
Click  Build Selected.
Build a surrounding air space along with domains for Perfectly matched layer (PML) that mimics the anechoic chamber.
Sphere 1 (sph1)
1
In the Geometry toolbar, click  Sphere.
2
In the Settings window for Sphere, locate the Size section.
3
In the Radius text field, type lda0.
4
Click to expand the Layers section. In the table, enter the following settings:
Layer name
Thickness (m)
Layer 1
0.5*arm_length
5
Click  Build Selected.
6
Click the  Wireframe Rendering button in the Graphics toolbar.
7
Click the  Zoom Extents button in the Graphics toolbar.
The volumetric region enclosed by antenna elements can be omitted for simplifying the physics setup.
Difference 1 (dif1)
1
In the Geometry toolbar, click  Booleans and Partitions and choose Difference.
2
Select the objects mov1(5) and sph1 only.
3
In the Settings window for Difference, locate the Difference section.
4
Find the Objects to subtract subsection. Click to select the  Activate Selection toggle button.
5
Select the objects mov1(1), mov1(2), mov1(3), mov1(4), mov1(6), and mov1(7) only.
6
Click  Build All Objects.
Add Material
1
In the Home toolbar, click  Add Material to open the Add Material window.
2
Go to the Add Material window.
3
In the tree, select Built-in>Air.
4
Click Add to Component in the window toolbar.
5
In the Home toolbar, click  Add Material to close the Add Material window.
Materials
PTFE
1
In the Materials toolbar, click  Blank Material.
2
Select Domain 6 only.
3
In the Settings window for Material, type PTFE in the Label text field.
4
Locate the Material Contents section. In the table, enter the following settings:
Property
Variable
Value
Unit
Property group
Relative permittivity
epsilonr_iso ; epsilonrii = epsilonr_iso, epsilonrij = 0
2.1
1
Basic
Relative permeability
mur_iso ; murii = mur_iso, murij = 0
1
1
Basic
Electrical conductivity
sigma_iso ; sigmaii = sigma_iso, sigmaij = 0
0
S/m
Basic
Definitions
Perfectly Matched Layer 1 (pml1)
1
In the Definitions toolbar, click  Perfectly Matched Layer.
PML acts as absorbing layer for EM wave. The far-field quantities are calculated at air-PML boundary interfaces.
2
Select Domains 1–4 and 7–10 only.
3
In the Settings window for Perfectly Matched Layer, locate the Geometry section.
4
From the Type list, choose Spherical.
Electromagnetic Waves, Frequency Domain (emw)
Lumped Port 1
1
In the Model Builder window, under Component 1 (comp1) right-click Electromagnetic Waves, Frequency Domain (emw) and choose Lumped Port.
2
Select Boundaries 37, 38, 46, and 51 only.
These boundaries are located at the middle of the feeder element.
3
In the Settings window for Lumped Port, locate the Boundary Selection section.
4
Click  Create Selection.
5
In the Create Selection dialog box, type Lumped port in the Selection name text field.
6
Click OK.
7
In the Settings window for Lumped Port, locate the Lumped Port Properties section.
8
From the Type of lumped port list, choose User defined.
9
In the hport text field, type gap_size.
10
In the wport text field, type r_antenna*pi*2.
11
Specify the ah vector as
0
x
0
y
1
z
Far-Field Domain 1
In the Physics toolbar, click  Domains and choose Far-Field Domain.
Mesh 1
In the Model Builder window, under Component 1 (comp1) right-click Mesh 1 and choose Build All.
Hide for Physics allows us to visualize the mesh and the rest of the results for internal geometric entities.
Definitions
Hide for Physics 1
1
In the Model Builder window, right-click View 1 and choose Hide for Physics.
2
In the Settings window for Hide for Physics, locate the Geometric Entity Selection section.
3
From the Geometric entity level list, choose Boundary.
4
Select Boundaries 6, 10, 69, 72, and 74 only.
Mesh 1
First, run a frequency domain study to analyze the far-field radiation of the antenna.
Study 1
Step 1: Frequency Domain
1
In the Model Builder window, under Study 1 click Step 1: Frequency Domain.
2
In the Settings window for Frequency Domain, locate the Study Settings section.
3
In the Frequencies text field, type 2.45.
4
In the Home toolbar, click  Compute.
Results
Multislice
1
In the Model Builder window, expand the Electric Field (emw) node, then click Multislice.
2
In the Settings window for Multislice, locate the Multiplane Data section.
3
Find the X-planes subsection. In the Planes text field, type 0.
4
Find the Z-planes subsection. In the Planes text field, type 0.
5
Click to expand the Range section. Select the Manual color range check box.
6
In the Minimum text field, type 0.
7
In the Maximum text field, type 500.
8
In the Electric Field (emw) toolbar, click  Plot.
9
Click the  Go to XZ View button in the Graphics toolbar.
Radiation Pattern 1
1
In the Model Builder window, expand the 2D Far Field (emw) node, then click Radiation Pattern 1.
2
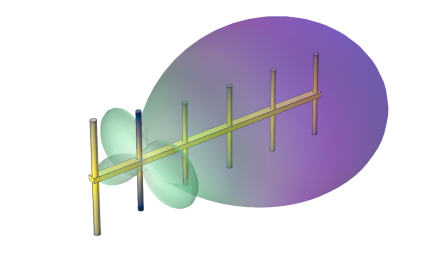
In the Settings window for Radiation Pattern, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Frequency Domain>Far field>emw.gaindBEfar - Far-field gain, dBi.
3
Locate the Evaluation section. Click Preview Evaluation Plane.
4
Click to expand the Legends section. From the Legends list, choose Manual.
5
In the table, enter the following settings:
Legends
H-plane
Radiation Pattern 2
1
Right-click Results>2D Far Field (emw)>Radiation Pattern 1 and choose Duplicate.
2
In the Settings window for Radiation Pattern, locate the Evaluation section.
3
Find the Normal vector subsection. In the y text field, type -1.
4
In the z text field, type 0.
5
Locate the Legends section. In the table, enter the following settings:
Legends
E-plane
6
In the 2D Far Field (emw) toolbar, click  Plot.
2D Far Field (emw)
1
In the Model Builder window, click 2D Far Field (emw).
2
In the Settings window for Polar Plot Group, locate the Axis section.
3
Select the Manual axis limits check box.
4
In the r maximum text field, type 15.
5
In the r minimum text field, type -25.
6
In the 2D Far Field (emw) toolbar, click  Plot.
Radiation Pattern 1
1
In the Model Builder window, expand the Results>3D Far Field, Gain (emw) node, then click Radiation Pattern 1.
2
In the Settings window for Radiation Pattern, locate the Expression section.
3
Select the Threshold check box. In the associated text field, type -20.
4
Click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Frequency Domain>Far field>emw.gaindBEfar - Far-field gain, dBi.
5
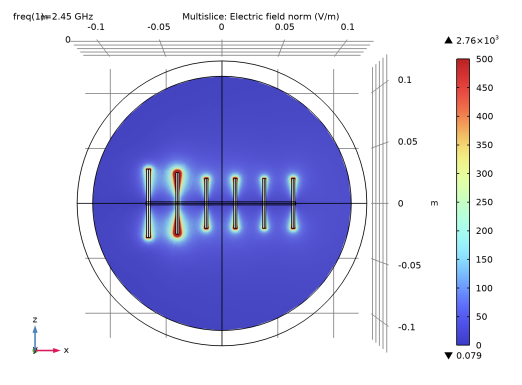
Locate the Evaluation section. Find the Angles subsection. In the Number of elevation angles text field, type 90.
6
In the Number of azimuth angles text field, type 90.
7
In the 3D Far Field, Gain (emw) toolbar, click  Plot.
8
Click the  Zoom Extents button in the Graphics toolbar.
Next, perform an adaptive frequency sweep to observe S-parameter responses for a wide band with a fine frequency step.
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Adaptive Frequency Sweep.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Study 2
Step 1: Adaptive Frequency Sweep
1
In the Settings window for Adaptive Frequency Sweep, locate the Study Settings section.
2
Click  Range.
3
In the Range dialog box, type 2.3[GHz] in the Start text field.
4
In the Stop text field, type 2.6[GHz].
5
Click Replace.
6
In the Settings window for Adaptive Frequency Sweep, locate the Values of Dependent Variables section.
7
Find the Store fields in output subsection. From the Settings list, choose For selections.
8
Under Selections, click  Add.
9
In the Add dialog box, select Lumped port in the Selections list.
Store fields in output for the selected lumped port boundaries reduces the size of the model file.
10
Click OK.
11
In the Model Builder window, click Study 2.
12
In the Settings window for Study, locate the Study Settings section.
13
Clear the Generate default plots check box.
14
In the Home toolbar, click  Compute.
Results
1D Plot Group 4
In the Home toolbar, click  Add Plot Group and choose 1D Plot Group.
Global 1
1
Right-click 1D Plot Group 4 and choose Global.
2
In the Settings window for Global, locate the Data section.
3
From the Dataset list, choose Study 2/Solution 2 (sol2).
4
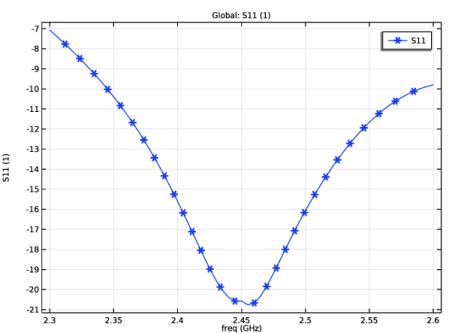
Click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Frequency Domain>Ports>emw.S11dB - S11.
5
Click to expand the Coloring and Style section. Find the Line markers subsection. From the Marker list, choose Asterisk.
6
From the Positioning list, choose Interpolated.
7
In the Number text field, type 30.
8
In the 1D Plot Group 4 toolbar, click  Plot.