
|
|
1
|
|
2
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material.
|
|
2
|
|
4
|
Click to expand the Material Properties section. In the Material properties tree, select Electromagnetic Models>Refractive Index>Refractive index, real part (n).
|
|
5
|
|
6
|
|
1
|
|
2
|
|
4
|
Click to expand the Material Properties section. In the Material properties tree, select Electromagnetic Models>Refractive Index>Refractive index, real part (n).
|
|
5
|
|
6
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Electromagnetic Waves, Frequency Domain (emw) click Wave Equation, Electric 1.
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
In the Mode analysis frequency text field, type c_const/1.55[um]. This frequency corresponds to a free space wavelength of 1.55 μm.
|
|
5
|
|
1
|
|
2
|
|
1
|
In the Model Builder window, expand the Results>Datasets node, then click Study 1/Solution 1 (sol1).
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
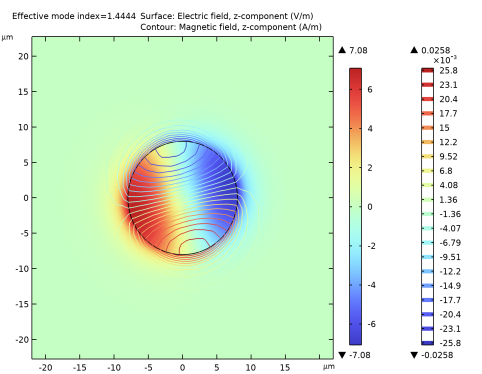
1
|
|
2
|
In the Settings window for Surface, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Frequency Domain>Electric>Electric field - V/m>emw.Ez - Electric field, z-component.
|
|
3
|
|
1
|
|
2
|
In the Settings window for Contour, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Frequency Domain>Magnetic>Magnetic field - A/m>emw.Hz - Magnetic field, z-component.
|
|
3
|