
|
 ,
,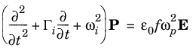 .
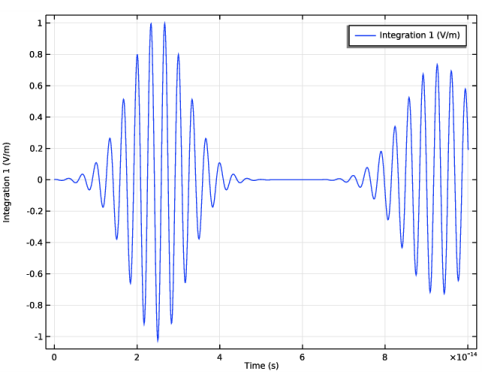
.
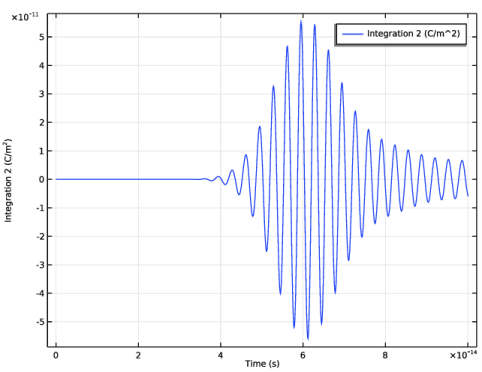
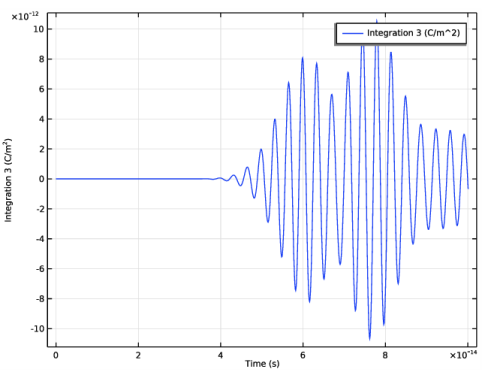

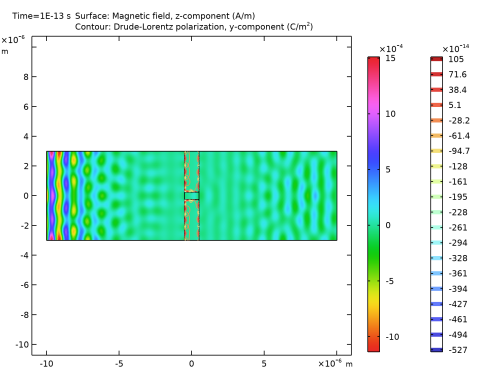
|
1
|
|
2
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Definitions and choose Variables.
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Geometry 1 right-click Rectangle 1 (r1) and choose Duplicate.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, under Component 1 (comp1) click Electromagnetic Waves, Transient (temw).
|
|
2
|
|
3
|
From the Electric field components solved for list, choose In-plane vector, to solve only for the in-plane components of the field.
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Electromagnetic Waves, Transient (temw) click Wave Equation, Electric 1.
|
|
2
|
|
3
|
|
4
|
|
5
|
In the Relative permittivity, high frequency table, enter 4 for the two first diagonal elements and keep 1 for the last one.
|
|
6
|
|
7
|
Locate the Magnetic Field section. From the μr list, choose User defined. Accept the default value 1.
|
|
8
|
Locate the Conduction Current section. From the σ list, choose User defined. Accept the default value 0.
|
|
1
|
|
2
|
In the Settings window for Drude-Lorentz Polarization, locate the Drude-Lorentz Dispersion Model section.
|
|
3
|
|
4
|
|
5
|
|
1
|
|
3
|
|
4
|
From the εr list, choose User defined. Locate the Magnetic Field section. From the μr list, choose User defined. Locate the Conduction Current section. From the σ list, choose User defined.
|
|
1
|
|
2
|
In the Settings window for Scattering Boundary Condition, locate the Scattering Boundary Condition section.
|
|
3
|
|
5
|
|
1
|
|
1
|
|
1
|
|
1
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
Click the Custom button.
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Study toolbar, click
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
Click OK.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|