PDF
Double-Pendulum Dynamics
Introduction
This tutorial model shows the modeling of a double pendulum using the Multibody Dynamics interface in COMSOL Multiphysics. The example begins with the creation of a simple hinge joint and then extends the model with several nodes available for joints such as constraints, locking, spring, damper, prescribed motion, and friction.
Model Definition
The model describes the motion of a double pendulum under gravity. The double pendulum system shown in Figure 1 behaves linearly for small angles of rotation, but it becomes highly nonlinear as the angle of rotation increases, eventually leading to a chaotic system.
Figure 1: Geometry of the double pendulum.
Here, the arms of the double pendulum are connected through a hinge joint. A hinge joint has one rotational degree of freedom about the joint axis. The remaining degrees of freedom of both components defining the joint are constrained to have the same values at the center of the joint.
The complete example is divided into six parts in order to illustrate the available functionality on the joint node and related subnodes.
A new study is added for each of the cases to provide more clarity. This also helps in storing all the model settings, which is needed when recomputing the solution in the solved model.
The different cases are as follows.
•
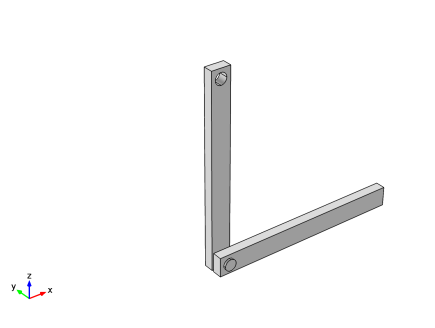
Case-1: Basic hinge joint
•
Case-2: Constraints on joint
•
Case-3: Locking on joint
•
Case-4: Spring and damper on joint
•
Case-5: Prescribed motion on joint
•
Case-6: Friction on joint
The details of each case along with the results and modeling instructions are given at a later point in this document.
Notes About the COMSOL Implementation
•
For the first three cases, both arms are modeled as flexible elements using the Linear Elastic Material model, and in the last three cases they are modeled as rigid elements using the Rigid Material model. Rigid elements can be used if the stresses and the deformation in the components are of no interest.
•
A Joint node can directly establish a connection between Rigid Material nodes. However, in flexible elements, Attachment nodes are needed to define the connection boundaries.
•
Constraint boundary conditions, like Rigid Connector and Fixed Constraint, cannot be used with the Rigid Material node. Hence, the Prescribed Displacement/Rotation node (subnode of Rigid Material) is used to prescribe the degrees of freedom.
Application Library path: Multibody_Dynamics_Module/Tutorials/double_pendulum
Model Definition: Case-1 (Basic Hinge Joint)
The top surface of the upper arm is constrained so that it cannot translate but it is free to rotate about the y-axis. The whole system is placed in the gravitational field to analyze the dynamics of the system.
In this case, the arms of the pendulum are modeled as flexible elements. Hence, the stresses generated in the components can be evaluated while computing the system’s dynamics.
Results and Discussion
Figure 2 and Figure 3 show the relative rotation between the arms and the reaction forces at the hinge joint during the oscillation of the double pendulum. The x and z components of the reaction forces balance the gravity load in the lower arm, as the pendulum oscillates in the xz-plane.
Figure 2: Relative rotation of the arms at the hinge joint (Case-1).
Figure 3: Reaction forces at the hinge joint (Case-1).
Model Definition: Case-2 (Constraints on Joint)
The top surface of the upper arm is fixed. A constraint is added at 45° relative rotation between both the arms. The whole system is placed in the gravitational field and the dynamics is analyzed.
Both arms are modeled as flexible parts. The deformation, as well as the stresses generated in the components, is significant during and after the activation of the constraint condition.
Results and Discussion
The relative rotation between the arms, when a constraint is added to the joint, is shown in Figure 4. In this case, the relative rotation first increases due to the gravitational force; then it decreases after reaching the constrained maximum limit as the lower arm bounces back. The relative rotation stays at its maximum limit for certain duration. This happens because of the bending of the flexible arms due to the high moment of inertia, and the sudden application of the constraint condition.
Figure 4: Relative rotation of the arms at the hinge joint (Case-2).
Figure 5: Reaction moments at the hinge joint (Case-2).
Figure 5 shows the reaction moments at the joint when using a constraint condition. The joint allows the arms to rotate about the y-axis, hence the reaction moment should be zero in this direction. However, when the constraint condition is active, the same joint restricts this motion and hence, a high reaction moment in the y direction can be seen. After the constraint condition has stopped the relative motion, the pendulum tries to rotate about other two axes due to its unsymmetrical geometry. Therefore, nonzero moments in these directions are also visible.
Figure 6 shows the variation of different forms of energy in the system when using a constraint condition. Before the constraint condition becomes active, potential energy is converted into kinetic energy and the strain energy is negligible. During the period when the constraint condition is active, the relative velocity goes to zero before changing sign. In this period, all kinetic energy is transformed into strain energy. When the constraint condition is no longer in action, the strain energy is converted back into kinetic energy. Structural waves persist in the components due to their flexible nature, therefore a nonzero strain energy can be seen.
Figure 6: Time variation of different forms of energy in Case-2.
Model Definition: Case-3 (Locking on Joint)
The top surface of the upper arm is constrained such that it cannot translate but is free to rotate about the y-axis. A lock condition is added at 45° relative rotation between both the arms of the pendulum. The whole system is placed in the gravitational field and the dynamics of the system is analyzed. Both the arms of the pendulum are modeled as flexible elements.
Results and Discussion
Figure 7 shows the relative rotation between the arms when a lock is present in the joint. In this case, the relative rotation first increases due to the gravitational force and then it is locked at the constrained maximum limit. The relative velocity is forced to zero for the rest of the simulation once the relative rotation reaches the lock position.
Figure 7: Relative rotation of the arms at the hinge joint (Case-3).
Figure 8 shows the reaction moments at the joint when a lock condition is used. The joint initially allows the arms to rotate relative to each other about the y-axis so that the reaction moment should be zero in this direction. However, after applying the lock condition, the same joint restricts this motion so that a high reaction moment in the y direction can be seen. After the lock condition is active, the pendulum also tries to rotate about the other two axes because of its unsymmetrical geometry. Therefore, nonzero moments in these directions are also visible.
Figure 8: Reaction moments at the hinge joint (Case-3).
Model Definition: Case-4 (Spring and Damper on Joint)
In this case, both arms of the pendulum are modeled as rigid elements. The upper arm is fixed. A torsional spring and damper are added on the relative rotation between the arms. The spring constant and the damping coefficient are 5e6 N-m and 1e6 N-m-s, respectively. The dynamics of the system is analyzed under gravity load.
Results and Discussion
Figure 9 shows the relative rotation between the arms when a spring and a damper are added to the joint. In this case, the torsional spring tries to restrict the relative motion at the joint and balances the moment caused by the gravity load. Without the damper the arms would oscillate about the equilibrium position. Here, a damper is added to the joint, so that the fluctuation in the relative rotation decreases and the arms tend to the equilibrium position.
Figure 9: Relative rotation of the arms at the hinge joint (Case-4).
Figure 10: Time variation of different forms of energy (Case-4).
Figure 10 shows the variation of different forms of energy in the system when a spring and damper are added to the joint. Initially, the potential energy is converted into kinetic energy. After some time, the spring and damper effects will however dominate. The damper dissipates energy and thus the kinetic energy is reduced to almost zero. As the energy dissipated in the damper is proportional to the velocity, it tends to a constant value. The energy stored in the spring is slowly converted into potential energy and vice-versa.
Model Definition: Case-5 (Prescribed Motion on Joint)
As in the previous case, arms of the pendulum are modeled as rigid elements. The upper arm is fixed. The relative angular velocity between both arms is prescribed for certain duration, after which each joint degree of freedom is made free. The prescribed angular velocity is a linear function of time (t rad/s) and reaches it’s maximum value 1 rad/s at 1 s.
Results and Discussion
Figure 11: Relative angular velocity of the arms at the hinge joint (Case-5).
Figure 11 shows the relative angular velocity between the arms when prescribed for the given duration. The velocity is prescribed until 1 s, and hence, it increases to it’s maximum value in this time interval. After that, due to the inertia of the components and without any losses, the velocity is maintained to the maximum value for the rest of the simulation. The relative rotation between the arms is shown in Figure 12. It is clear from this plot that before 1 s, the rotation increases quadratically with time, after which time it increases linearly.
Figure 12: Relative rotation of the arms at the hinge joint (Case-5).
Model Definition: Case-6 (Friction on Joint)
As in the previous case, the arms of the pendulum are modeled as rigid bodies. The upper arm is fixed. The dynamics of the system is analyzed under gravity load and with frictional losses in the joint. The effective friction moment is computed using the forces acting on a joint and it is applied on the relative rotation between the arms.
Results and Discussion
Figure 13: Relative rotation of the arms at the hinge joint (Case-6).
Figure 13 shows the relative rotation between the arms. The decay in the magnitude of relative rotation due to the frictional losses at the hinge joint, can be seen.
The time variation of the friction moment is shown in Figure 14. The average value of friction moment is governed by the gravity load acting on both the arms and the fluctuations in friction moment are governed by the inertial forces in both the arms. A fast variation in the friction moment can be seen when the direction of motion is getting reversed. This mimics the behavior of Coulomb’s friction law, but the friction moment is not fully discontinuous as it would be in Coulomb’s friction law.
Figure 15 shows the variation of different forms of energy in the system when frictional losses are added to the joint. The increasing frictional energy loss can be seen in the plot.
Figure 14: Friction moment profile at the hinge joint (Case-6).
Figure 15: Time variation of different forms of energy (Case-6).
Modeling Instructions (Basic Hinge Joint)
From the File menu, choose New.
New
In the New window, click  Model Wizard.
Model Wizard
1
In the Model Wizard window, click  3D.
2
In the Select Physics tree, select Structural Mechanics>Multibody Dynamics (mbd).
3
Click Add.
4
Click  Study.
5
In the Select Study tree, select General Studies>Time Dependent.
6
Click  Done.
Geometry 1
If you do not want to build the geometry step by step, you can load it from the stored model: In the Model Builder window, under Component 1 (comp1) right-click Geometry 1 and choose Insert Sequence. Browse to the model’s Application Libraries folder and double-click the file double_pendulum.mph. You can then continue to the Definitions section below.
To build the geometry from scratch, continue here.
Block 1 (blk1)
1
In the Geometry toolbar, click  Block.
2
In the Settings window for Block, locate the Size and Shape section.
3
In the Depth text field, type 0.5.
4
In the Height text field, type 10.
Cylinder 1 (cyl1)
1
In the Geometry toolbar, click  Cylinder.
2
In the Settings window for Cylinder, locate the Size and Shape section.
3
In the Radius text field, type 0.3.
4
In the Height text field, type 0.5.
5
Locate the Position section. In the x text field, type 0.5.
6
In the z text field, type 9.5.
7
Locate the Axis section. From the Axis type list, choose y-axis.
Difference 1 (dif1)
1
In the Geometry toolbar, click  Booleans and Partitions and choose Difference.
2
Select the object blk1 only.
3
In the Settings window for Difference, locate the Difference section.
4
Find the Objects to subtract subsection. Click to select the  Activate Selection toggle button.
5
Select the object cyl1 only.
Cylinder 2 (cyl2)
1
In the Geometry toolbar, click  Cylinder.
2
In the Settings window for Cylinder, locate the Size and Shape section.
3
In the Radius text field, type 0.3.
4
In the Height text field, type 1.25.
5
Locate the Position section. In the x text field, type 0.5.
6
In the y text field, type -0.75.
7
In the z text field, type 0.5.
8
Locate the Axis section. From the Axis type list, choose y-axis.
Copy 1 (copy1)
1
In the Geometry toolbar, click  Transforms and choose Copy.
2
Select the object cyl2 only.
Block 2 (blk2)
1
In the Geometry toolbar, click  Block.
2
In the Settings window for Block, locate the Size and Shape section.
3
In the Width text field, type 10.
4
In the Depth text field, type 0.5.
5
Locate the Position section. In the y text field, type -0.625.
Difference 2 (dif2)
1
In the Geometry toolbar, click  Booleans and Partitions and choose Difference.
2
Select the object blk2 only.
3
In the Settings window for Difference, locate the Difference section.
4
Find the Objects to subtract subsection. Click to select the  Activate Selection toggle button.
5
Select the object copy1 only.
Union 1 (uni1)
1
In the Geometry toolbar, click  Booleans and Partitions and choose Union.
2
Select the objects cyl2 and dif1 only.
3
In the Settings window for Union, locate the Union section.
4
Clear the Keep interior boundaries check box.
Form Union (fin)
1
In the Model Builder window, under Component 1 (comp1)>Geometry 1 click Form Union (fin).
2
In the Settings window for Form Union/Assembly, locate the Form Union/Assembly section.
3
From the Action list, choose Form an assembly.
4
Click  Build Selected.
Definitions
Integration 1 (intop1)
1
In the Definitions toolbar, click  Nonlocal Couplings and choose Integration.
2
Click in the Graphics window and then press Ctrl+A to select both domains.
Variables 1
1
In the Definitions toolbar, click  Local Variables.
2
In the Settings window for Variables, locate the Variables section.
3
In the table, enter the following settings:
Name
Expression
Unit
Description
Wp
intop1(mbd.rho*g_const*w)
J
Potential energy
Add Material
1
In the Home toolbar, click  Add Material to open the Add Material window.
2
Go to the Add Material window.
3
In the tree, select Built-in>Structural steel.
4
Click Add to Component in the window toolbar.
5
In the Home toolbar, click  Add Material to close the Add Material window.
Multibody Dynamics (mbd)
Gravity 1
In the Model Builder window, under Component 1 (comp1) right-click Multibody Dynamics (mbd) and choose Gravity.
Attachment 1
1
In the Physics toolbar, click  Boundaries and choose Attachment.
2
Select Boundaries 19, 20, 24, and 25 only.
Hinge Joint 1
1
In the Physics toolbar, click  Global and choose Hinge Joint.
2
In the Settings window for Hinge Joint, locate the Attachment Selection section.
3
From the Source list, choose Fixed.
4
From the Destination list, choose Attachment 1.
5
Locate the Axis of Joint section. Specify the e0 vector as
0
x
1
y
0
z
6
Locate the Joint Forces and Moments section. From the list, choose Do not compute.
As first attachment, select the boundaries of the protruding cylinder.
Attachment 2
1
In the Physics toolbar, click  Boundaries and choose Attachment.
2
Select Boundaries 16, 17, 22, and 23 only.
As second attachment, select the interior boundaries of the hole in the outer bar.
Attachment 3
1
In the Physics toolbar, click  Boundaries and choose Attachment.
2
Select Boundaries 6–9 only.
Hinge Joint 2
1
In the Physics toolbar, click  Global and choose Hinge Joint.
2
In the Settings window for Hinge Joint, locate the Attachment Selection section.
3
From the Source list, choose Attachment 2.
4
From the Destination list, choose Attachment 3.
5
Locate the Axis of Joint section. Specify the e0 vector as
0
x
1
y
0
z
Study 1
Step 1: Time Dependent
1
In the Model Builder window, under Study 1 click Step 1: Time Dependent.
2
In the Settings window for Time Dependent, locate the Study Settings section.
3
In the Output times text field, type range(0,0.02,1.5).
4
In the Model Builder window, click Study 1.
5
In the Settings window for Study, type Study: Basic in the Label text field.
6
In the Home toolbar, click  Compute.
Results
Displacement (mbd)
The two default plots show the displacement and velocity profile in the arms of the double pendulum. The stresses can also be visualized by changing the expression in the first plot.
Add the point trajectories in the Displacement plot to visualize the direction of the motion of each arm.
Point Trajectories 1
1
In the Displacement (mbd) toolbar, click  More Plots and choose Point Trajectories.
2
Select Points 14 and 21 only.
3
In the Settings window for Point Trajectories, locate the Coloring and Style section.
4
Find the Line style subsection. From the Type list, choose Tube.
Color Expression 1
1
Right-click Point Trajectories 1 and choose Color Expression.
2
In the Settings window for Color Expression, locate the Expression section.
3
In the Expression text field, type t.
4
Locate the Coloring and Style section. Clear the Color legend check box.
5
Click the  Go to Default View button in the Graphics toolbar.
Use the following instructions to reproduce Figure 2:
Relative rotation
1
In the Home toolbar, click  Add Plot Group and choose 1D Plot Group.
2
In the Settings window for 1D Plot Group, type Relative rotation in the Label text field.
Global 1
1
Right-click Relative rotation and choose Global.
2
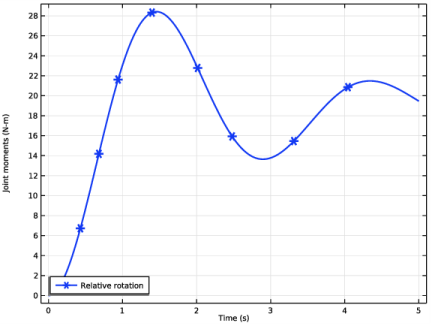
In the Settings window for Global, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Multibody Dynamics>Hinge joints>Hinge Joint 2>mbd.hgj2.th - Relative rotation - rad.
3
Locate the y-Axis Data section. In the table, enter the following settings:
Expression
Unit
Description
mbd.hgj2.th
deg
Relative rotation
4
Click to expand the Title section. From the Title type list, choose None.
5
Click to expand the Legends section. Clear the Show legends check box.
6
Click to expand the Coloring and Style section. From the Width list, choose 2.
7
In the Relative rotation toolbar, click  Plot.
To generate the joint forces plot given in Figure 3, follow the instructions below:
Joint forces
1
In the Home toolbar, click  Add Plot Group and choose 1D Plot Group.
2
In the Settings window for 1D Plot Group, type Joint forces in the Label text field.
Global 1
1
Right-click Joint forces and choose Global.
2
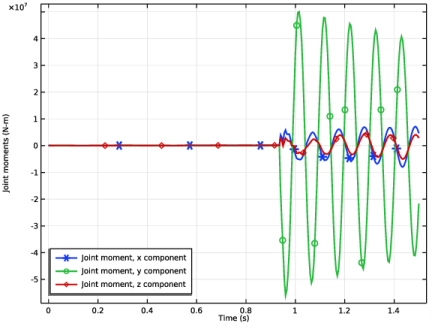
In the Settings window for Global, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Multibody Dynamics>Hinge joints>Hinge Joint 2>Joint force - N>mbd.hgj2.Fx - Joint force, x component.
3
Click Add Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Multibody Dynamics>Hinge joints>Hinge Joint 2>Joint force - N>mbd.hgj2.Fy - Joint force, y component.
4
Click Add Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Multibody Dynamics>Hinge joints>Hinge Joint 2>Joint force - N>mbd.hgj2.Fz - Joint force, z component.
5
Locate the Title section. From the Title type list, choose None.
6
Locate the Coloring and Style section. From the Width list, choose 2.
7
Find the Line markers subsection. From the Marker list, choose Cycle.
8
From the Positioning list, choose Interpolated.
Joint forces
1
In the Model Builder window, click Joint forces.
2
In the Settings window for 1D Plot Group, locate the Plot Settings section.
3
Select the y-axis label check box. In the associated text field, type Joint forces (N).
4
Locate the Legend section. From the Position list, choose Upper left.
5
In the Joint forces toolbar, click  Plot.
Joint forces in the joint’s local coordinate system can also be plotted by doing similar steps.
Modeling Instructions (Constraints on Joint)
The same hinge joint is used for the first three cases by controlling its subnodes at the study node. The joint’s center and axis are computed with different techniques. This is to demonstrate various types of techniques available, where each one can be useful in certain cases.
Multibody Dynamics (mbd)
Hinge Joint 2
1
In the Model Builder window, under Component 1 (comp1)>Multibody Dynamics (mbd) click Hinge Joint 2.
2
In the Settings window for Hinge Joint, locate the Center of Joint section.
3
From the list, choose User defined.
4
Specify the Xc vector as
0.5
x
0
y
0.5
z
5
Locate the Axis of Joint section. From the list, choose From selected coordinate system.
6
From the Axis to use list, choose 2.
Constraints 1
1
In the Physics toolbar, click  Attributes and choose Constraints.
2
In the Settings window for Constraints, locate the Rotational Constraints section.
3
In the θmax text field, type pi/4.
The relative motion between the source and destination in the first hinge joint should be set to zero.
Hinge Joint 1
In the Model Builder window, under Component 1 (comp1)>Multibody Dynamics (mbd) click Hinge Joint 1.
Prescribed Motion 1
In the Physics toolbar, click  Attributes and choose Prescribed Motion.
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select General Studies>Time Dependent.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Study 2
Step 1: Time Dependent
1
In the Settings window for Time Dependent, locate the Study Settings section.
2
In the Output times text field, type range(0,0.01,1.5).
3
In the Model Builder window, click Study 2.
4
In the Settings window for Study, type Study: Constraints in the Label text field.
5
Locate the Study Settings section. Clear the Generate default plots check box.
6
In the Home toolbar, click  Compute.
Duplicate the plots generated in the first case to reproduce the results shown in Figure 4 and Figure 5:
Results
Relative rotation: Constraints
1
In the Model Builder window, right-click Relative rotation and choose Duplicate.
2
In the Settings window for 1D Plot Group, type Relative rotation: Constraints in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study: Constraints/Solution 2 (sol2).
4
In the Relative rotation: Constraints toolbar, click  Plot.
Joint moments: Constraints
1
In the Model Builder window, right-click Joint forces and choose Duplicate.
2
In the Settings window for 1D Plot Group, type Joint moments: Constraints in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study: Constraints/Solution 2 (sol2).
Global 1
1
In the Model Builder window, expand the Joint moments: Constraints node, then click Global 1.
2
In the Settings window for Global, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Multibody Dynamics>Hinge joints>Hinge Joint 2>Joint moment - N·m>mbd.hgj2.Mx - Joint moment, x component.
3
Click Add Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Multibody Dynamics>Hinge joints>Hinge Joint 2>Joint moment - N·m>mbd.hgj2.My - Joint moment, y component.
4
Click Add Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Multibody Dynamics>Hinge joints>Hinge Joint 2>Joint moment - N·m>mbd.hgj2.Mz - Joint moment, z component.
Joint moments: Constraints
1
In the Model Builder window, click Joint moments: Constraints.
2
In the Settings window for 1D Plot Group, locate the Legend section.
3
From the Position list, choose Lower left.
4
Locate the Plot Settings section. In the y-axis label text field, type Joint moments (N-m).
5
In the Joint moments: Constraints toolbar, click  Plot.
Follow these instructions to reproduce energy plot shown in Figure 6:
Energy: Constraints
1
Right-click Joint moments: Constraints and choose Duplicate.
2
In the Settings window for 1D Plot Group, type Energy: Constraints in the Label text field.
Global 1
1
In the Model Builder window, expand the Energy: Constraints node, then click Global 1.
2
In the Settings window for Global, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Definitions>Variables>Wp - Potential energy - J.
3
Click Add Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Multibody Dynamics>Global>mbd.Wk_tot - Total kinetic energy - J.
4
Click Add Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Multibody Dynamics>Global>mbd.Ws_tot - Total elastic strain energy - J.
Energy: Constraints
1
In the Model Builder window, click Energy: Constraints.
2
In the Settings window for 1D Plot Group, locate the Legend section.
3
From the Position list, choose Upper left.
4
Locate the Plot Settings section. In the y-axis label text field, type Energy (J).
5
In the Energy: Constraints toolbar, click  Plot.
Modeling Instructions (Locking on Joint)
Multibody Dynamics (mbd)
Hinge Joint 2
1
In the Model Builder window, under Component 1 (comp1)>Multibody Dynamics (mbd) click Hinge Joint 2.
2
In the Settings window for Hinge Joint, locate the Axis of Joint section.
3
From the list, choose Select a parallel edge.
Joint Axis 1
1
In the Model Builder window, click Joint Axis 1.
2
Select Edge 33 only.
Hinge Joint 2
1
In the Model Builder window, click Hinge Joint 2.
2
In the Settings window for Hinge Joint, locate the Center of Joint section.
3
From the list, choose Centroid of selected entities.
4
From the Entity level list, choose Edge.
Center of Joint: Edge 1
1
In the Model Builder window, click Center of Joint: Edge 1.
2
Select Edges 34, 35, 46, and 48 only.
Hinge Joint 2
In the Model Builder window, click Hinge Joint 2.
Locking 1
1
In the Physics toolbar, click  Attributes and choose Locking.
2
In the Settings window for Locking, locate the Rotational Locking section.
3
In the θmax text field, type pi/4.
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select General Studies>Time Dependent.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Study 3
Step 1: Time Dependent
1
In the Settings window for Time Dependent, locate the Study Settings section.
2
In the Output times text field, type range(0,0.005,1.5).
3
Locate the Physics and Variables Selection section. Select the Modify model configuration for study step check box.
4
In the tree, select Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 1>Prescribed Motion 1 and Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 2>Constraints 1.
5
Right-click and choose Disable.
6
In the Model Builder window, click Study 3.
7
In the Settings window for Study, type Study: Locking in the Label text field.
8
Locate the Study Settings section. Clear the Generate default plots check box.
Solution 3 (sol3)
1
In the Study toolbar, click  Show Default Solver.
2
In the Model Builder window, expand the Solution 3 (sol3) node, then click Time-Dependent Solver 1.
3
In the Settings window for Time-Dependent Solver, click to expand the Time Stepping section.
4
From the Steps taken by solver list, choose Intermediate.
5
In the Model Builder window, expand the Study: Locking>Solver Configurations>Solution 3 (sol3)>Time-Dependent Solver 1 node, then click Fully Coupled 1.
6
In the Settings window for Fully Coupled, click to expand the Method and Termination section.
7
From the Nonlinear method list, choose Automatic (Newton).
8
In the Study toolbar, click  Compute.
To generate the relative rotation plot shown in Figure 7, follow the instruction below:
Results
Relative rotation: Locking
1
In the Model Builder window, right-click Relative rotation and choose Duplicate.
2
In the Settings window for 1D Plot Group, type Relative rotation: Locking in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study: Locking/Solution 3 (sol3).
4
In the Relative rotation: Locking toolbar, click  Plot.
To generate a plot for joint moments shown in Figure 8, follow the instructions below:
Joint moments: Locking
1
In the Model Builder window, right-click Joint moments: Constraints and choose Duplicate.
2
In the Settings window for 1D Plot Group, type Joint moments: Locking in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study: Locking/Solution 3 (sol3).
4
In the Joint moments: Locking toolbar, click  Plot.
Modeling Instructions (Spring and Damper on Joint)
The hinge joint used in the previous cases could be used here to define the connection between the rigid components. A new hinge joint is however created so that it is easy to rerun each study independently without changing the attachment selection in the hinge joint.
Multibody Dynamics (mbd)
Rigid Material 1
1
In the Physics toolbar, click  Domains and choose Rigid Material.
2
Select Domain 2 only.
Use the Rigid Material’s subnode to prescribe or constrain its motion.
Fixed Constraint 1
In the Physics toolbar, click  Attributes and choose Fixed Constraint.
Rigid Material 2
1
In the Physics toolbar, click  Domains and choose Rigid Material.
2
Select Domain 1 only.
Hinge Joint 3
1
In the Physics toolbar, click  Global and choose Hinge Joint.
2
In the Settings window for Hinge Joint, locate the Attachment Selection section.
3
From the Source list, choose Rigid Material 1.
4
From the Destination list, choose Rigid Material 2.
5
Locate the Center of Joint section. From the list, choose User defined.
6
Specify the Xc vector as
0.5
x
0
y
0.5
z
7
Locate the Axis of Joint section. Specify the e0 vector as
0
x
1
y
0
z
Spring and Damper 1
1
In the Physics toolbar, click  Attributes and choose Spring and Damper.
2
In the Settings window for Spring and Damper, locate the Spring and Damper: Rotational section.
3
In the kθ text field, type 5e6.
4
In the cθ text field, type 1e6.
Add an ODE to calculate the energy dissipated in damper.
5
Click the  Show More Options button in the Model Builder toolbar.
6
In the Show More Options dialog box, in the tree, select the check box for the node Physics>Equation-Based Contributions.
7
Click OK.
Energy: Damper
1
In the Physics toolbar, click  Global and choose Global Equations.
2
In the Settings window for Global Equations, type Energy: Damper in the Label text field.
3
Locate the Global Equations section. In the table, enter the following settings:
Name
f(u,ut,utt,t) (1)
Initial value (u_0) (1)
Initial value (u_t0) (1/s)
Description
Wd
d(Wd,t)-mbd.hgj3.Qdamper
0
0
Energy dissipated in damper
4
Locate the Units section. Click  Select Dependent Variable Quantity.
5
In the Physical Quantity dialog box, type energy in the text field.
6
Click  Filter.
7
In the tree, select General>Energy (J).
8
Click OK.
9
In the Settings window for Global Equations, locate the Units section.
10
Click  Select Source Term Quantity.
11
In the Physical Quantity dialog box, type power in the text field.
12
Click  Filter.
13
In the tree, select General>Power (W).
14
Click OK.
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select General Studies>Time Dependent.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Study 4
Step 1: Time Dependent
1
In the Settings window for Time Dependent, locate the Study Settings section.
2
In the Output times text field, type range(0,0.02,5).
3
Locate the Physics and Variables Selection section. Select the Modify model configuration for study step check box.
4
In the tree, select Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 1.
5
Right-click and choose Disable.
6
In the tree, select Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Attachment 1, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Attachment 2, and Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Attachment 3.
7
Right-click and choose Disable.
8
In the tree, select Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 2.
9
Right-click and choose Disable.
10
In the Model Builder window, click Study 4.
11
In the Settings window for Study, type Study: Spring-Damper in the Label text field.
12
Locate the Study Settings section. Clear the Generate default plots check box.
13
In the Home toolbar, click  Compute.
Follow the instructions to generate the relative rotation plot shown in Figure 9:
Results
Relative rotation 1
In the Model Builder window, right-click Relative rotation and choose Duplicate.
Relative rotation: Spring-Damper
1
In the Settings window for 1D Plot Group, type Relative rotation: Spring-Damper in the Label text field.
Set the Dataset to None for now to avoid the error in automatic plotting of a variable, which is not available in the selected dataset.
2
Locate the Data section. From the Dataset list, choose None.
Global 1
1
In the Model Builder window, expand the Relative rotation: Spring-Damper node, then click Global 1.
2
In the Settings window for Global, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Multibody Dynamics>Hinge joints>Hinge Joint 3>comp1.mbd.hgj3.th - Relative rotation - rad.
3
Locate the y-Axis Data section. In the table, enter the following settings:
Expression
Unit
Description
comp1.mbd.hgj3.th
deg
Relative rotation
Relative rotation: Spring-Damper
1
In the Model Builder window, click Relative rotation: Spring-Damper.
2
In the Settings window for 1D Plot Group, locate the Data section.
3
From the Dataset list, choose Study: Spring-Damper/Solution 4 (sol4).
4
In the Relative rotation: Spring-Damper toolbar, click  Plot.
The energy plot in Figure 10 can be generated by following the steps below:
Energy: Spring-Damper
1
In the Home toolbar, click  Add Plot Group and choose 1D Plot Group.
2
In the Settings window for 1D Plot Group, type Energy: Spring-Damper in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study: Spring-Damper/Solution 4 (sol4).
Global 1
1
Right-click Energy: Spring-Damper and choose Global.
2
In the Settings window for Global, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Definitions>Variables>Wp - Potential energy - J.
3
Click Add Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Multibody Dynamics>Global>mbd.Wk_tot - Total kinetic energy - J.
4
Locate the y-Axis Data section. In the table, enter the following settings:
Expression
Unit
Description
mbd.hgj3.Wspring
J
Energy stored in spring
Wd
J
Energy dissipated in damper
5
Locate the Title section. From the Title type list, choose None.
6
Locate the Coloring and Style section. From the Width list, choose 2.
7
Find the Line markers subsection. From the Marker list, choose Cycle.
8
From the Positioning list, choose Interpolated.
Energy: Spring-Damper
1
In the Model Builder window, click Energy: Spring-Damper.
2
In the Settings window for 1D Plot Group, locate the Plot Settings section.
3
Select the y-axis label check box. In the associated text field, type Energy (J).
4
In the Energy: Spring-Damper toolbar, click  Plot.
5
Locate the Axis section. Select the Manual axis limits check box.
6
In the y maximum text field, type 1e6.
7
In the Energy: Spring-Damper toolbar, click  Plot.
Modeling Instructions (Prescribed Motion on Joint)
Multibody Dynamics (mbd)
Hinge Joint 3
In the Model Builder window, under Component 1 (comp1)>Multibody Dynamics (mbd) click Hinge Joint 3.
Prescribed Motion 1
1
In the Physics toolbar, click  Attributes and choose Prescribed Motion.
2
In the Settings window for Prescribed Motion, locate the Prescribed Rotational Motion section.
3
From the Prescribed motion through list, choose Angular velocity.
4
In the ωp text field, type t.
5
From the Activation condition list, choose Conditionally active.
6
In the iθp text field, type t>1.
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select General Studies>Time Dependent.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Study 5
Step 1: Time Dependent
1
In the Settings window for Time Dependent, locate the Study Settings section.
2
In the Output times text field, type range(0,0.02,2).
3
Locate the Physics and Variables Selection section. Select the Modify model configuration for study step check box.
4
In the tree, select Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Gravity 1, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Attachment 1, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 1, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Attachment 2, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Attachment 3, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 2, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 3>Spring and Damper 1, and Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Energy: Damper.
5
Right-click and choose Disable.
6
In the Model Builder window, click Study 5.
7
In the Settings window for Study, type Study: Prescribed motion in the Label text field.
8
Locate the Study Settings section. Clear the Generate default plots check box.
9
In the Home toolbar, click  Compute.
Follow these instructions to generate the relative velocity (Figure 11) and the relative rotation (Figure 12) plots:
Results
Relative rotation: Prescribed motion
1
In the Model Builder window, right-click Relative rotation: Spring-Damper and choose Duplicate.
2
In the Settings window for 1D Plot Group, type Relative rotation: Prescribed motion in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study: Prescribed motion/Solution 5 (sol5).
4
In the Relative rotation: Prescribed motion toolbar, click  Plot.
Relative velocity: Prescribed motion
1
Right-click Relative rotation: Spring-Damper and choose Duplicate.
2
In the Settings window for 1D Plot Group, type Relative velocity: Prescribed motion in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study: Prescribed motion/Solution 5 (sol5).
Global 1
1
In the Model Builder window, expand the Relative velocity: Prescribed motion node, then click Global 1.
2
In the Settings window for Global, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Multibody Dynamics>Hinge joints>Hinge Joint 3>mbd.hgj3.th_t - Relative angular velocity - rad/s.
3
Locate the y-Axis Data section. In the table, enter the following settings:
Expression
Unit
Description
mbd.hgj3.th_t
deg/s
Relative angular velocity
Relative velocity: Prescribed motion
1
In the Model Builder window, click Relative velocity: Prescribed motion.
2
In the Relative velocity: Prescribed motion toolbar, click  Plot.
Modeling Instructions (Friction on Joint)
Multibody Dynamics (mbd)
Hinge Joint 3
Compute joint forces to evaluate normal force in the friction node.
1
In the Model Builder window, under Component 1 (comp1)>Multibody Dynamics (mbd) click Hinge Joint 3.
2
In the Settings window for Hinge Joint, locate the Joint Forces and Moments section.
3
From the list, choose Computed using weak constraints.
Friction 1
1
In the Physics toolbar, click  Attributes and choose Friction.
2
In the Settings window for Friction, locate the Friction section.
3
In the μ text field, type 0.6.
4
In the r text field, type 0.3.
Add an ODE to calculate the energy loss due to friction.
Energy: Friction
1
In the Model Builder window, right-click Energy: Damper and choose Duplicate.
2
In the Settings window for Global Equations, type Energy: Friction in the Label text field.
3
Locate the Global Equations section. In the table, enter the following settings:
Name
f(u,ut,utt,t) (W)
Initial value (u_0) (J)
Initial value (u_t0) (W)
Description
Wf
d(Wf,t)-mbd.hgj3.Qfriction
0
0
Energy loss due to friction
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select General Studies>Time Dependent.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Study 6
Step 1: Time Dependent
1
In the Settings window for Time Dependent, locate the Study Settings section.
2
In the Output times text field, type range(0,0.05,10).
3
Locate the Physics and Variables Selection section. Select the Modify model configuration for study step check box.
4
In the tree, select Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Attachment 1, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 1, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Attachment 2, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Attachment 3, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 2, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 3>Spring and Damper 1, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 3>Prescribed Motion 1, and Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Energy: Damper.
5
Right-click and choose Disable.
6
In the Model Builder window, click Study 6.
7
In the Settings window for Study, type Study: Friction in the Label text field.
8
Locate the Study Settings section. Clear the Generate default plots check box.
Solution 6 (sol6)
1
In the Study toolbar, click  Show Default Solver.
2
In the Model Builder window, expand the Solution 6 (sol6) node.
3
In the Model Builder window, expand the Study: Friction>Solver Configurations>Solution 6 (sol6)>Dependent Variables 1 node, then click Energy loss due to friction (comp1.ODE1).
4
In the Settings window for State, locate the Scaling section.
5
From the Method list, choose Manual.
6
In the Scale text field, type 1e6.
7
In the Study toolbar, click  Compute.
Follow the instructions below to generate the relative rotation and friction moment plots shown in Figure 13 and Figure 14 respectively:
Results
Relative rotation: Friction
1
In the Model Builder window, right-click Relative rotation: Spring-Damper and choose Duplicate.
2
In the Settings window for 1D Plot Group, type Relative rotation: Friction in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study: Friction/Solution 6 (sol6).
4
In the Relative rotation: Friction toolbar, click  Plot.
Friction moment
1
Right-click Relative rotation: Friction and choose Duplicate.
2
In the Settings window for 1D Plot Group, type Friction moment in the Label text field.
Global 1
1
In the Model Builder window, expand the Friction moment node, then click Global 1.
2
In the Settings window for Global, locate the y-Axis Data section.
3
In the table, enter the following settings:
Expression
Unit
Description
mbd.hgj3.fric1.Mf
N*m
Friction moment
Friction moment
1
In the Model Builder window, click Friction moment.
2
In the Friction moment toolbar, click  Plot.
The energy plot in Figure 15 can be generated by following the steps below:
Energy: Friction
1
In the Home toolbar, click  Add Plot Group and choose 1D Plot Group.
2
In the Settings window for 1D Plot Group, type Energy: Friction in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study: Friction/Solution 6 (sol6).
4
From the Time selection list, choose Interpolated.
5
In the Times (s) text field, type range(0,0.2,10).
Global 1
1
Right-click Energy: Friction and choose Global.
2
In the Settings window for Global, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Definitions>Variables>Wp - Potential energy - J.
3
Click Add Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Multibody Dynamics>Global>mbd.Wk_tot - Total kinetic energy - J.
4
Locate the y-Axis Data section. In the table, enter the following settings:
Expression
Unit
Description
Wf
J
Energy loss due to friction
5
Locate the Title section. From the Title type list, choose None.
6
Locate the Coloring and Style section. From the Width list, choose 2.
7
Find the Line markers subsection. From the Marker list, choose Cycle.
8
From the Positioning list, choose Interpolated.
Energy: Friction
1
In the Model Builder window, click Energy: Friction.
2
In the Settings window for 1D Plot Group, locate the Plot Settings section.
3
Select the y-axis label check box. In the associated text field, type Energy (J).
4
In the Energy: Friction toolbar, click  Plot.
5
Locate the Axis section. Select the Manual axis limits check box.
6
In the y maximum text field, type 3e6.
7
In the Energy: Friction toolbar, click  Plot.
You can also generate an animation of the double pendulum. Follow the steps given below to generate the animation for Case-1:
Animation 1
1
In the Results toolbar, click  Animation and choose Player.
2
In the Settings window for Animation, locate the Frames section.
3
In the Number of frames text field, type 50.
4
Click the  Play button in the Graphics toolbar.
The analyses are now finished. If you want to store this model and reuse it later, you need to disable the nodes in all the studies that are added at a later stage.
Study: Prescribed motion
Step 1: Time Dependent
1
In the Model Builder window, under Study: Prescribed motion click Step 1: Time Dependent.
2
In the Settings window for Time Dependent, locate the Physics and Variables Selection section.
3
In the tree, select Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 3>Friction 1 and Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Energy: Friction.
4
Right-click and choose Disable.
Study: Spring-Damper
Step 1: Time Dependent
1
In the Model Builder window, under Study: Spring-Damper click Step 1: Time Dependent.
2
In the Settings window for Time Dependent, locate the Physics and Variables Selection section.
3
In the tree, select Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 3>Prescribed Motion 1, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 3>Friction 1, and Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Energy: Friction.
4
Right-click and choose Disable.
Study: Locking
Step 1: Time Dependent
1
In the Model Builder window, under Study: Locking click Step 1: Time Dependent.
2
In the Settings window for Time Dependent, locate the Physics and Variables Selection section.
3
In the tree, select Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Rigid Material 1, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Rigid Material 2, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 3, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Energy: Damper, and Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Energy: Friction.
4
Right-click and choose Disable.
Study: Constraints
Step 1: Time Dependent
1
In the Model Builder window, under Study: Constraints click Step 1: Time Dependent.
2
In the Settings window for Time Dependent, locate the Physics and Variables Selection section.
3
Select the Modify model configuration for study step check box.
4
In the tree, select Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 2>Locking 1, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Rigid Material 1, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Rigid Material 2, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 3, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Energy: Damper, and Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Energy: Friction.
5
Right-click and choose Disable.
Study: Basic
Step 1: Time Dependent
1
In the Model Builder window, under Study: Basic click Step 1: Time Dependent.
2
In the Settings window for Time Dependent, locate the Physics and Variables Selection section.
3
Select the Modify model configuration for study step check box.
4
In the tree, select Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 1>Prescribed Motion 1, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 2>Constraints 1, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 2>Locking 1, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Rigid Material 1, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Rigid Material 2, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Hinge Joint 3, Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Energy: Damper, and Component 1 (comp1)>Multibody Dynamics (mbd), Controls spatial frame>Energy: Friction.
5
Right-click and choose Disable.