
|
|
Δτ/2+0.20σn (MPa)
|
Δτ/2+0.27σn (MPa)
|
Δσn(MPa)
|
|
|
1
|
|
2
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
Click in the Graphics window and then press Ctrl+A to select both objects.
|
|
3
|
|
1
|
|
2
|
On the object csol1, select Point 5 only.
|
|
3
|
|
4
|
|
1
|
|
2
|
Select the object fil1 only.
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
Click in the Graphics window and then press Ctrl+A to select both objects.
|
|
3
|
|
4
|
|
5
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Geometry 1 right-click Work Plane 1 (wp1) and choose Revolve.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material.
|
|
2
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Solid Mechanics (solid) and choose Fixed Constraint.
|
|
1
|
|
1
|
|
2
|
|
3
|
Specify the F vector as
|
|
4
|
|
1
|
|
2
|
|
3
|
Specify the M vector as
|
|
4
|
|
1
|
In the Model Builder window, under Global Definitions>Load and Constraint Groups click Load Group 1.
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, under Global Definitions>Load and Constraint Groups click Load Group 2.
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
Click Add four times.
|
|
6
|
|
1
|
|
2
|
|
1
|
|
3
|
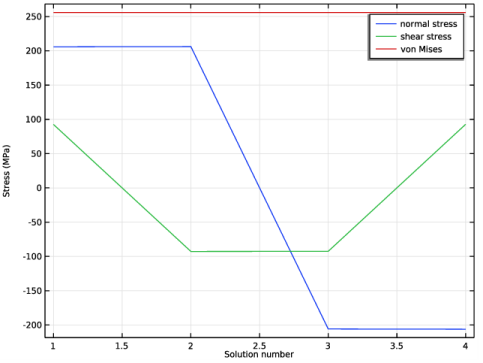
In the Settings window for Point Graph, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Solid Mechanics>Stress (Gauss points)>Second Piola-Kirchhoff stress, Gauss point evaluation (material and geometry frames) - N/m²>solid.SGpYY - Second Piola-Kirchhoff stress, Gauss point evaluation, YY-component.
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Legends section. In the table, enter the following settings:
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Legends section. In the table, enter the following settings:
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
Find the Physics interfaces in study subsection. In the table, clear the Solve check box for Study 1.
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
Find the Physics interfaces in study subsection. In the table, clear the Solve check box for Study 1.
|
|
4
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
Find the Physics interfaces in study subsection. In the table, clear the Solve check box for Study 1.
|
|
4
|
|
5
|
|
1
|
|
2
|
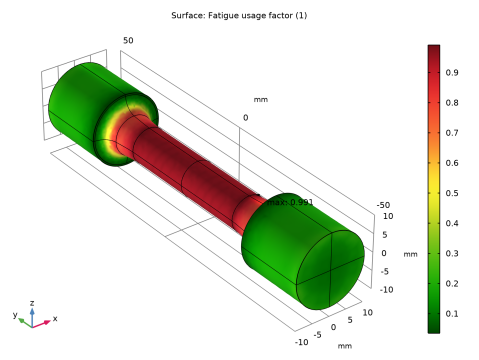
Right-click Component 1 (comp1)>Fatigue Normal Stress and choose the boundary evaluation Stress-Based.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
Find the Physics interfaces in study subsection. In the table, clear the Solve check box for Solid Mechanics (solid).
|
|
4
|
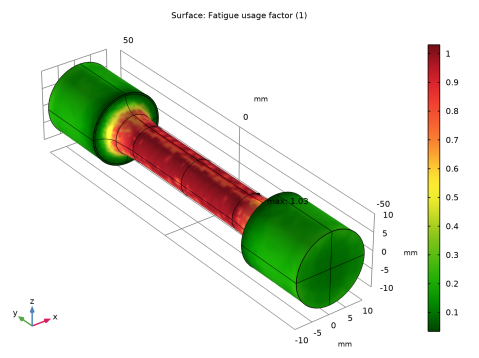
Find the Studies subsection. In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Fatigue.
|
|
5
|
|
6
|
|
1
|
|
2
|
Find the Values of variables not solved for subsection. From the Settings list, choose User controlled.
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
In the Settings window for 3D Plot Group, type Fatigue Usage Factor (Matake) in the Label text field.
|
|
1
|
|
2
|
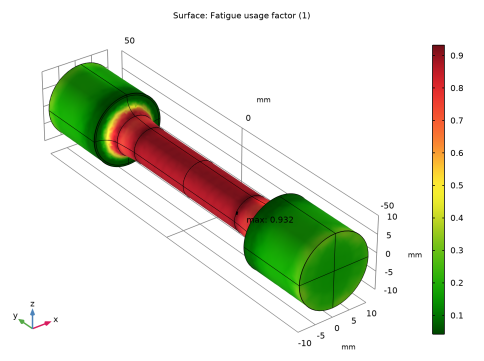
In the Settings window for 3D Plot Group, type Fatigue Usage Factor (Normal Stress) in the Label text field.
|