
|
|
νx = 0.19
|
|
|
νy = 0.021
|
|
|
νz = 0.021
|
|
|
1
|
|
2
|
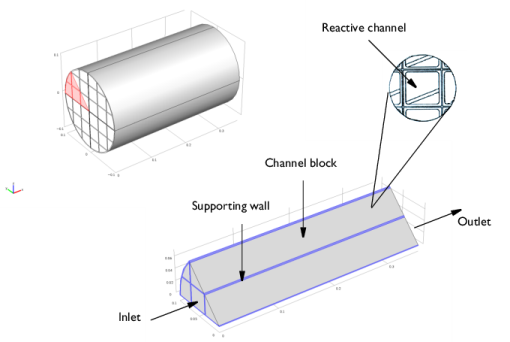
In the Application Libraries window, select Chemical Reaction Engineering Module>Tutorials>monolith_3d in the tree.
|
|
3
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
Find the Physics interfaces in study subsection. In the table, clear the Solve check boxes for Study 1 and Study 2.
|
|
5
|
|
1
|
|
2
|
|
3
|
Find the Studies subsection. In the Select Study tree, select Preset Studies for Some Physics Interfaces>Stationary.
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
In the Model Builder window, under 3D Model (comp2) right-click Solid Mechanics (solid) and choose Material Models>Linear Elastic Material.
|
|
2
|
|
3
|
|
4
|
Locate the Linear Elastic Material section. From the E list, choose User defined. In the associated text field, type 1.5e9.
|
|
5
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, under 3D Model (comp2)>Solid Mechanics (solid) click Linear Elastic Material 1.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
1
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
In the table, clear the Solve for check boxes for Reaction Engineering (re), Chemistry 1 (chem), Transport of Diluted Species in Porous Media (tds), Heat Transfer in Porous Media 1 (ht), and Darcy’s Law 1 (dl).
|
|
4
|
Click to expand the Values of Dependent Variables section. Find the Values of variables not solved for subsection. From the Settings list, choose User controlled.
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
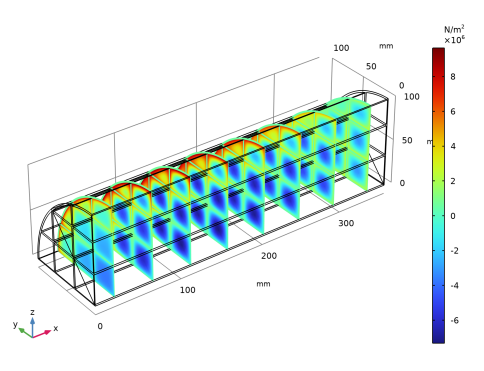
In the Settings window for Slice, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose 3D Model (comp2)>Solid Mechanics>Stress>Stress tensor (spatial frame) - N/m²>solid.sxx - Stress tensor, xx-component.
|
|
3
|
|
4
|
|
5
|