
|
|
1
|
|
2
|
In the Application Libraries window, select Battery Design Module>Batteries, Lithium-Ion>lib_base_model_1d in the tree.
|
|
3
|
Click
|
|
1
|
|
2
|
|
1
|
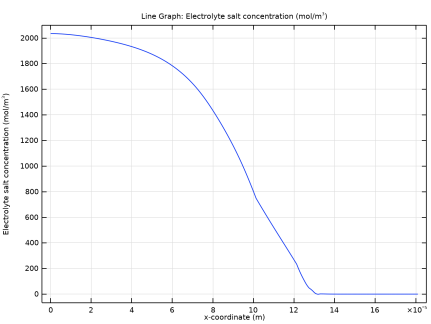
In the Model Builder window, expand the Component 1 (comp1)>Lithium-Ion Battery (liion) node, then click Electrode Current Density 1.
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Cumulative Energy (ge) click Global Equations 1.
|
|
2
|
|
4
|
|
5
|
In the Dependent variable quantity table, enter the following settings:
|
|
6
|
|
7
|
In the Source term quantity table, enter the following settings:
|
|
1
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
Click
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
Right-click Study 1>Solver Configurations>Solution 1 (sol1)>Time-Dependent Solver 1 and choose Stop Condition.
|
|
9
|
|
10
|
|
11
|
|
12
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
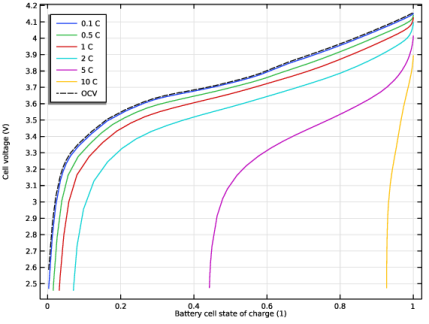
In the Settings window for Global, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Definitions>E_cell - Point Probe 1 - V.
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
In the Settings window for Global, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Definitions>Variables>E_ocv_cell - Open-circuit cell voltage - V.
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
9
|
Click to expand the Coloring and Style section. Find the Line style subsection. From the Line list, choose Dashed.
|
|
10
|
|
11
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
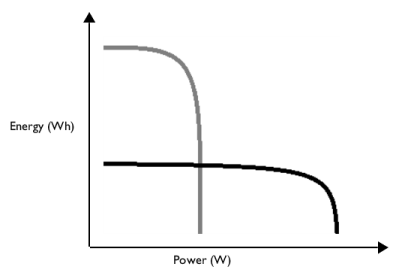
In the Settings window for Global Evaluation, type Ragone Plot Data Evaluation in the Label text field.
|
|
3
|
|
4
|
Locate the Expressions section. In the table, enter the following settings:
|
|
5
|
|
1
|
|
2
|
In the Settings window for Table, type Ragone Plot Data Energy Optimized Cell in the Label text field.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
10
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
In the Model Builder window, under Study 1>Solver Configurations right-click Parametric Solutions 1 (sol2) and choose Solution>Copy.
|
|
1
|
In the Model Builder window, under Study 1>Solver Configurations click Parametric Solutions 1 - Copy 1 (sol9).
|
|
2
|
In the Settings window for Solution, type Parametric Solutions - Energy Optimized Cell in the Label text field.
|
|
3
|
|
1
|
|
2
|
|
1
|
In the Model Builder window, under Results>Derived Values right-click Ragone Plot Data Evaluation and choose Evaluate>New Table.
|
|
1
|
|
2
|
In the Settings window for Table, type Ragone Plot Data for Power Optimized Cell in the Label text field.
|
|
1
|
In the Model Builder window, under Results>Ragone Plots right-click Table Graph 1 and choose Duplicate.
|
|
2
|
|
3
|
|
4
|
Locate the Legends section. In the table, enter the following settings:
|
|
5
|
|
1
|
|
2
|
|
1
|
|
2
|