The charge relaxation is modeled using the polarization current (Ref. 1)

where τm is the relaxation time, and Δεm is the relative permittivity contribution. Note that both quantities can be taken as diagonal matrices to cover the anisotropic case.

Equation 3-3 can be integrated once with respect to time assuming zero initial fields

By applying the divergence operator, Equation 3-1 yields the current conservation equation:

Assume that the electric conductivity is small, so that the induction current can be neglected. Using Equation 3-5, the current conservation equation can be written as

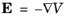
Equation 3-6 can be solved using the scalar electric potential V as a dependent variable determine the electric field as , and it needs to be solved together with N vector Equation 3-4 for N vector dependent variables em. In time domain, these auxiliary field variables can be treated as the local state variables, and each of N corresponding ODE equations can be integrated locally.

In frequency domain, Equation 3-5 for the auxiliary variables can be solved analytically, so that Equation 3-6 gives

where ω is the angular frequency. By separating the real and imaginary parts, the equation can be further rewritten as

Each term in the sum in the above equations represents a pole on the complex w plane. Thus, the model is referred to as Multipole Debye Dispersion model. To determine the number of poles needed to approximate the lossy material behavior can be a difficult task. One possible approach is presented in Constant loss tangent section.

Instead, one can solve N algebraic equations for the auxiliary variables em

together with Equation 3-7. Even though this approach requires extra degrees of freedom, it will produce frequency independent contributions to the damping and stiffness matrices. The corresponding linear damped eigenvalue problem can be solved using the default solver in a single run for any specified number of eigenfrequencies which will be computed exactly.

In Ref. 2, a special parameterization was suggested for the multipole Debye model based on the original result derived in Ref. 3 for equivalent electric circuits. It allows to fit the model parameters for Multipole Debye Model so that the loss tangent is nearly constant at a certain frequency range.

The input parameters are the loss tangent η(fc) together with the center frequency fc, at which is has been measured, and the model bandwidth nd that defines a frequency interval (in decades) centered at fc, in which the loss tangent will be approximately constant and equal to η(fc).

where N is the number of Debye poles, and .

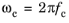
where k > 1 is the spacing parameter. Note that the relative electric permittivity in the low and high frequency limits are related simply as .

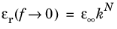
COMSOL Multiphysics software will automatically deduce the necessary number of poles N together with the values of the relaxation times tm and relative permittivity contributions Δεm, which will be used in computations to maintain the requested bandwidth and accuracy.

which requires poles, and the spacing parameter with the loss angle d computed from η(fc).

Thus computed parameters will be used automatically in a Time Dependent study using Equation 3-4, and in an Eigenfrequency study using Equation 3-8.

where αT(T) is a temperature-dependent shift function.

The implication is that the problem can be solved using the original material data, provided that the time is transformed into the reduced time. Think of the shift function αT(T) as a multiplier to the relaxation time in Equation 3-4 and Equation 3-8.

here, a base-e logarithm is used, Q is the activation energy (SI unit: J/mol), and R is the universal gas constant. Temperature T0 is the temperature at which the relaxation time would becomes infinite.

here, a base-e logarithm is used, Q is the activation energy (SI unit: J/mol), and R is the universal gas constant.

The first step to compute the shift function αT(T) consists of building a master curve based on experimental data. To do this, the curves of the dielectric properties versus time or frequency are measured at a reference temperature Tref. Then, the same properties are measured at different temperatures.

The shift value of each curve, with respect to the master curve obtained at the temperature Tref, defines the shift factor αT(T). The constants C1 and C2 are material dependent and are calculated after plotting log(αT) versus T − Tref.

Since the master curve is measured at an arbitrary reference temperature Tref, the shift factor αT(T) can be derived with respect to any temperature, and it is commonly taken as the shift with respect to the glass transition temperature.

here, a base-e logarithm is used, Q is the activation energy (SI unit: J/mol), R is the universal gas constant, T is the current temperature, Tref is a reference temperature, χ is a dimensionless activation energy fraction, and Tf is the so-called fictive temperature. The fictive temperature is given as the weighted average of partial fictive temperatures.

Here, wi are the weights and Tfi are the partial fictive temperatures. The partial fictive temperatures are determined from a system of coupled ordinary differential equations (ODEs) which follow Tool’s equation

here, λ0i is a relaxation time parameter.