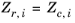You are viewing the documentation for an older COMSOL version. The latest version is
available here.
An equation of state (EOS) model is an algebraic relation between the absolute pressure (P),
the molar volume (
V), and the absolute temperature (
T). An equation of state that is at least cubic in volume and in the form of
(2-8)
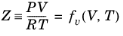
where Z is the compressibility factor and
R the universal gas constant, can be used to describe both gases and liquids. The cubic equations of state are widely used to describe the gaseous and liquid volumetric behavior of pure fluids and also all other properties with extensions to mixtures. A comprehensive comparison of different cubic EOS models can be found in
Ref. 2 and
Ref. 3.
(2-9)
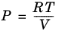
(2-10)
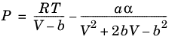
(2-11)
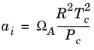
(2-12)
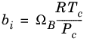
(2-13)
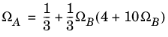
(2-14)
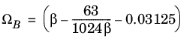
(2-15)
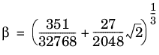
(2-16)
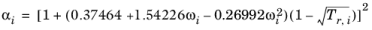
(2-17)
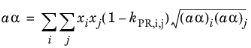
(2-18)
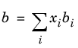
The binary interaction parameters (BIPs), kPR, are symmetric with zeros in the diagonal:
(2-19)
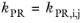
(2-20)
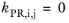
For the Twu modification (Ref. 6) of the Peng–Robinson model, the alpha function,
αi, is replaced by
(2-21)
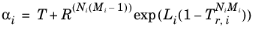
The binary interaction parameters kPR, are used for the Twu modification. Acentric factor,
ωi, is not used in this model but critical temperature and critical pressure must be specified for all species. The species specific fit parameters
Li,
Mi,
Ni can be determined by fitting the pure species phase equilibrium to the vapor pressure curve.
(2-22)
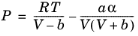
(2-23)
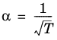
(2-24)
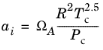
(2-25)
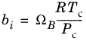
(2-26)
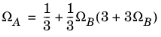
(2-27)
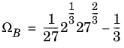
(2-28)
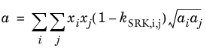
(2-29)
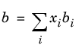
The binary interaction parameters, kSRK, are symmetric with zero in the diagonal:
(2-30)
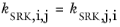
(2-31)
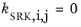
If a value is missing for kSRK,i,j in the database, it is set to zero (a warning node is created). The values for critical temperature,
Tc, critical pressure,
Pc, and acentric factor,
ωi, must be specified for all species. The Soave–Redlich–Kwong equation of state is a version of
Equation 2-22 modified by Soave
Ref. 8, where for pure species
i, the alpha function is modified to
(2-32)
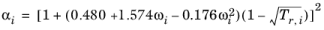
The Graboski and Daubert Ref. 9 modification of the Soave–Redlich–Kwong equation of state replaces alpha function by
(2-33)
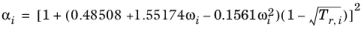
except for H2, where it is replaced by
(2-34)
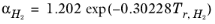
(2-35)
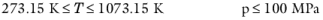
(2-36)
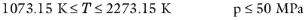
The following water and steam properties, available by creating a Species Property, are computed using the IAPWS correlations: density, volume, enthalpy, internal energy, Helmholtz energy, heat capacity at constant pressure, and heat capacity at constant volume. The amounts present in the vapor and liquid phase can be computed using an
Equilibrium Calculation.
(2-37)
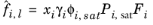
(2-38)
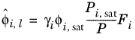
where the activity coefficient, γi, describes the nonideal liquid phase and
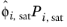
is the fugacity at the vapor-liquid phase boundary at equilibrium for the pure species
i. The Poynting correction,
Fi, describes the pure species fugacity deviation from the boiling curve and can be expressed as
(2-39)
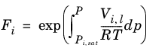
(2-40)
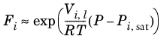
(2-41)
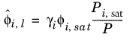
(2-42)
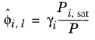
(2-43)
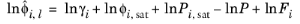
(2-44)
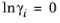
(2-45)
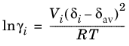
where Vi is species molar volume and
δi is species solubility parameter, and
δav is
(2-46)
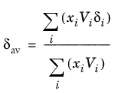
The volume parameter, Vi, is set equal the liquid volume,
Vi,l,b at normal boiling point which must be specified for all species. The solubility parameter,
δi must be specified for all species and can be estimated from the normal heat of vaporization,
ΔHvap,i and the liquid volume at normal boiling point as below:
(2-47)
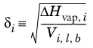
(2-48)
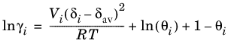
(2-49)
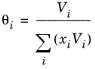
Wilson Ref. 17 derived his activity coefficient model from a consideration of probabilities of neighboring molecules in a liquid
(2-50)
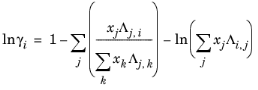
(2-51)
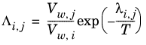
where the Wilson volume parameter, Vw,i, is a species-specific parameter describing volume. If the volume parameter is not available, the liquid volume at normal boiling point is used. The Wilson binary interaction parameters
λi,j are specified in terms of absolute temperature. The binary interaction parameter matrix is nonsymmetric and with zeros in its diagonal. All off-diagonal values must be specified
(2-52)
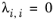
(2-53)
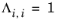
Renon and Prausnitz (Ref. 18) formulated a three parameter activity coefficient model that is able to describe liquid-liquid equilibrium; the nonrandom two-liquid (NRTL) model:
(2-54)
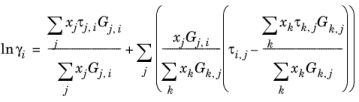
(2-55)
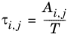
(2-56)
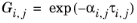
The three parameters are Ai,j,
Aj,i, and
αi,j. A more general form is implemented here:
(2-57)
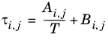
(2-58)
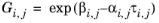
The binary interaction parameters, Ai,j, are specified in terms of absolute temperature. The diagonal values are zero and the matrix is nonsymmetric. All off-diagonal values must be specified.
The binary interaction parameters, Bi,j, have values of zero on the diagonal and the matrix is nonsymmetric. For each pair of species, at least
Ai,j or
Bi,j should be specified.
The randomness parameters, αi,j, have values of zero on the diagonal and the matrix is symmetric. All off-diagonal values must be specified. Alternatively one can set the more generic form directly specifying parameter
βi,j for which diagonal values are zero and the matrix is nonsymmetric. For each pair of species at least
αi,j or
βi,j should be specified.
(2-59)
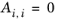
(2-60)
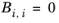
(2-61)
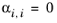
(2-62)
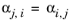
(2-63)
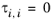
(2-64)
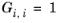
(2-65)
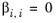
(2-66)
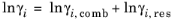
(2-67)
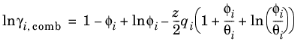
(2-68)
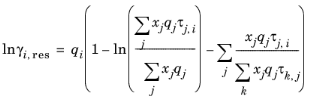
(2-69)
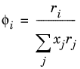
(2-70)
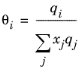
(2-71)
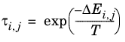
The coordination number is taken equal to z = 10. The binary interaction energy parameters,
ΔEi,j, are specified in terms of absolute temperature (K). The diagonal values are zero and the matrix is nonsymmetric. All off-diagonal values must be specified.
(2-72)
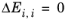
(2-73)
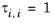
The volume parameters, ri and surface area parameters,
qi are model-specific parameters for each species. If the parameters are not specified, they can be derived from the van der Waals volume,
VVDW,i, and area,
AVDW,i, respectively
(2-74)
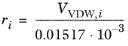
(2-75)
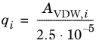
For all species ri or
VVDW,i and
qi or
AVDW,i must be specified.
The UNIQUAC Functional-group Activity Coefficients (UNIFAC; see Ref. 20) uses the same equations as UNIQUAC but the parameters are constructed from group contributions. The model can be used if UNIQUAC parameters are not available for all species. The activity coefficients are calculated from
Equation 2-66. The combinatorial part follows from equation
Equation 2-67, where
(2-76)
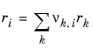
(2-77)
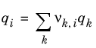
where rk and
qk are the values for group
k in species
i, and
νk,i is the number of occurrences of group
k in molecule. The residual term in
Equation 2-66 is calculated from a summation over functional groups:
(2-78)
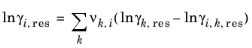
The values for ln(γk,res) are calculated from the mixture containing all species at a specified composition x. The values for ln(
γi,k,res) are calculated for a mixture of group k considering only pure species
i. Both are defined, for functional group
k, by
(2-79)
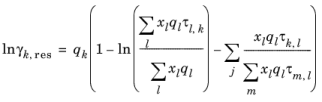
where xl and
xm are the compositions of functional group
l and
m in the mixture
(2-80)
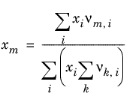
(2-81)
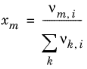
The volume parameters rk and surface area parameters
qk are model-specific parameters for each group. The binary interaction between groups
k and
m is
(2-82)
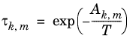
The binary interaction parameters, Ak,m, are specified in terms of absolute temperature. The diagonal values are zero, the matrix is nonsymmetric. All off-diagonal values must be specified.
The default group and interaction parameters are those published by the UNIFAC consortium (Ref. 21 through
Ref. 26), with added groups from Balslev and Abildskov (
Ref. 27) but can be modified per package or database. The groups must be specified for all species. Note that the interaction parameter matrix is sparse, and a package can only be used if all interaction parameters for all used groups are specified.
The Chao–Seader model Ref. 13 correlates liquid phase partial coefficients for pure species, for use of hydrogen and hydrocarbon mixtures at elevated pressure and temperatures. It is expressed by
(2-83)
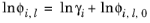
The activity is based on the Scatchard–Hildebrand equation Ref. 14 and presented in
Equation 2-45 to
Equation 2-47. Chao–Seader specific values for liquid volume,
Vi and solubility parameter,
δi are used.
If Vi is unspecified, it can be estimated by
If the Chao–Seader specific solubility parameter, δi, is not specified, the generic solubility parameter is used.
(2-84)
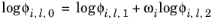
(2-85)
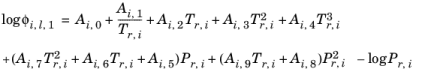
(2-86)
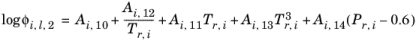
A Chao–Seader specific acentric factor ωi is used. If it is unknown, it can be set equal to the generic acentric factor. The parameter values are taken from the later publication of Grayson and Streed
Ref. 15 and given in
Table 2-2.
|
-
|
0.5 < Tr,i < 1.3, for all hydrocarbons except CH 4
|
(2-87)
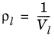
(2-88)
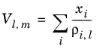
Hankinson and Thomson Ref. 28 presented the Corresponding States Liquid Density (COSTALD) equation as
(2-89)
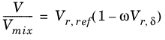
(2-90)
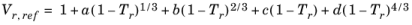
(2-91)
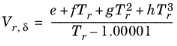
(2-92)
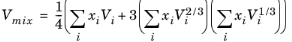
(2-93)
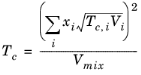
(2-94)
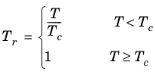
(2-95)
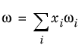
where the volume, Vi and acentric factor,
ωi for species
i are model specific parameters. If the COSTALD volume parameter is unspecified, it is estimated from the van der Waals volume when
VVDW,i> 0.3
×10
-3 m
3/mol
(2-96)
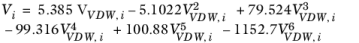
(2-97)
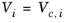
If the COSTALD acentric factor, ωi is not specified, it can be set equal to the generic acentric factor for species
i. A critical temperature,
Tc,i must be specified for all species.
The Rackett equation Ref. 29 computes the liquid density at the saturation point, and can be used to describe liquid density at any pressure using the assumption that the liquid is incompressible. The equation and its condition can be expressed as:
(2-98)
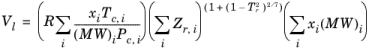
(2-99)
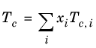
(2-100)
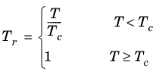
Critical temperatures, Tc,i, critical pressures,
Pc,i, and molecular weights,
Mi, must be specified for all species. The model parameter,
Zr,i, must be specified for all species. If the value is not available it can be set to the critical compressibility factor:
(2-101)