The following correlations correspond to equations 9.26 and 9.27 in Ref. 21:

where the height of the wall, L, is a correlation input.

All material properties are evaluated at (T + Text) ⁄ 2, except ρs, which is evaluated at the wall temperature, T, and g is the acceleration of gravity equal to 9.81 m/s2. This correlation is valid for 104≤ RaL ≤ 1013. The laminar-turbulent transition at RaL = 109 is handled by the use of a smoothed Heaviside function with a transition of size 108, which corresponds to 10% of the threshold value.

The following correlations correspond to equations 9.26 and 9.27 in Ref. 21 (the same as for a vertical wall):

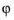
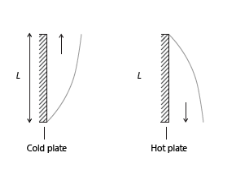
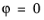
where the length of the wall, L, is a correlation input and is the tilt angle (the angle between the wall and the vertical direction; for vertical walls). These correlations are valid for −60° < 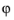 < 60° and 104≤ RaL ≤ 1013.

The definition of the Raleigh number, RaL, is analogous to the one for vertical walls and is given by the following:

g denotes the gravitational acceleration, equal to 9.81 m/s2.

For turbulent flow, 1 is used instead of cos 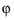 in the expression for h, because this gives better accuracy (see Ref. 41).

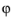
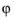
The laminar-turbulent transition depends on (see Ref. 41). Unfortunately, little data is available about transition. There is some data available in Ref. 41 but this data is only approximate, according to the authors. In addition, data is only provided for water (Pr around 6). For this reason, the flow is defined as turbulent, independently of the value, when

All material properties are evaluated at (T + Text) ⁄ 2, except ρswhich is evaluated at the wall temperature, T. The laminar-turbulent transition at RaL = 109 is handled by the use of a smoothed Heaviside function with a transition of size 108, which corresponds to 10% of the threshold value.

The following correlations correspond to equations 9.30–9.32 in Ref. 21 but can also be found as equations 7.77 and 7.78 in Ref. 41.

If ρ < ρext, then

while if ρ ≥ ρext, then

RaL is given by Equation 4-179 or Equation 4-180, and L, the characteristic length (defined as area/perimeter, see Ref. 41) is a correlation input. The material data are evaluated at (T + Text) ⁄ 2, except ρswhich is evaluated at the wall temperature, T.

When the density depends only on temperature, the conditions ρ < ρext and ρ ≥ ρext can be replaced by T > Text and T ≤ Text respectively.

The laminar-turbulent transition at RaL = 107 is handled by the use of a smoothed Heaviside function with a transition of size 106, which corresponds to 10% of the threshold value.

Equation 4-184 is used when ρ ≥ ρext (or T ≤ Text) and Equation 4-185 is used when ρ < ρext (or T > Text). Otherwise it is the same implementation as for Horizontal Plate, Upside.

The following correlations correspond to equations 9.34 in Ref. 21. It is validated for RaD ≤ 1012.

Here D is the cylinder diameter and RaD is given by

The material data are evaluated at (T + Text) ⁄2, except ρswhich is evaluated at the wall temperature, T.

The following correlations correspond to equation 9.35 in Ref. 21. It is validated for RaD ≤ 1011 and Pr ≥ 0.7.

Here D is the cylinder diameter and RaD is given by

The material data are evaluated at (T + Text) ⁄2, except ρswhich is evaluated at the wall temperature, T.

The following correlation corresponds to equation 7.83 in Ref. 41. It evaluates the heat transfer coefficient on the lateral surface of the thin cylinder. The horizontal disks (top and bottom) should be treated as horizontal plates.

where D is the cylinder diameter, H is the cylinder height, and RaH is given by

The material data are evaluated at (T + Text) ⁄2, except ρswhich is evaluated at the wall temperature, T.

If the thermal boundary layer thickness δT is much smaller than the cylinder diameter D, the curvature does not play any significant role, and vertical wall correlations should be used. In practice, the (δT < D) criterion requires