A complication when modeling the water-ion-polymer system is that the water-ion friction forces need to be taken into account in the transport equations both for the ions as well as the water molecules. The Weber-Newman model (Ref. 7) is based on concentrated solution theory, taking into account all three binary interactions between the charge-carrying ion, the immobilized polymer matrix and the water molecules. The model introduces the chemical potential of water in the polymer μ0 (J/mol) as dependent variable, and defines the polymer water flux, N0 (mol/(m2·s)), as

where ξ (dimensionless) is the electroosmotic coefficient and α (mol2/(J·m·s)) the water transport coefficient, with the mass balance

where a0 is the thermodynamic activity of water, VH2O is the partial molar volume of water, and pH2O(l) is the liquid water pressure. VH2O is defined as

where MH2O is the molar mass and ρH2O is the density of water at the operating temperature.

By integration, the chemical potential μ0 is then defined as

where μ0,ref is a chosen reference potential, for convenience set to 0.

For a vapor-equilibrated membrane, the parameters σl, ξ, and α typically all depend on the polymer water content. When measuring water uptake and other polymer electrolyte properties (such as σl, ξ, and α), it is common to report these versus the water activity, aw, which is not the same as the thermodynamic activity a0.

In the gas phase, aw is defined as follows

where is the pH2O(g) is the partial water pressure, pvap is the vapor pressure, and pg is the gas pressure. At an interface between a polymer electrolyte and the gas phase, assuming the polymer phase to be in equilibrium with the gas phase (and ideal gas conditions), the following condition holds

where is the standard condition gas pressure (typically 1 atm or 1 bar). The corresponding water activity inside the polymer electrolyte for a vapor-equilibrated polymer, for which the liquid pressure pH2O(l) is 0, may hence be defined as

For a liquid-equilibrated system aw is equal to 1.

Gas diffusion electrodes typically have a large electrolyte-gas phase interface area, in combination with fairly short diffusion lengths in the transport direction perpendicular to the pore walls. The water activity in the polymer of the gas diffusion electrode may be approximated to always be in equilibrium with the adjacent gas phase in the pores. Hence the expression for aw in the gas phase may be used also for the polymer in gas diffusion electrodes, and μ0 need not to be solved for explicitly.

As a result of the definition of the chemical potential, both the liquid pressure and the thermodynamic activity of water need to be considered when defining boundary conditions for water absorption-desorption at a Membrane boundary.

For a membrane in contact with vapor, the liquid pressure pH2O(l) is 0 Pa, and the chemical potential μ0 relates to the thermodynamic activity a0 as

Experimentally, the interface between a membrane and the vapor phase is often seen to exhibit a mass transfer resistance, where the absorption rate rabs,dsp follows a relationship based on the difference in the thermodynamic water activity between the two phases, as follows

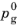
where kabs,dsp (mol/(m2 s)) is a rate constant and the activity of water in the gas phase has been assumed to equal the partial pressure pH2O(g) divided by the standard condition pressure (ideal gas conditions).

For a membrane in contact with liquid water, aw is equal to 1. Interfaces of this kind have been empirically found to exhibit way lower mass transfer resistances than for the vapor case. For this case, the boundary condition may be formulated based on the liquid pressure pH2O(l) as

For this cases the absorption rate rabs,dsp may be evaluated at the boundary as

The boundary heat source Qb due to the absorption-desorption is defined as