You are viewing the documentation for an older COMSOL version. The latest version is
available here.
The purpose of the Modal Solver and the
Model Reduction is to speed up certain simulations by performing a model reduction using eigenpairs, making use of the solution to an eigenvalue or eigenfrequency problem to construct a basis using eigenvectors corresponding to the dominant dynamics. That is, the solution of the underlying system of equations is approximated by a linear combination of parametric or time-dependent coefficients and a few dominant eigenvectors. Optionally this basis can be extended with
constraint modes. Each constraint mode is a solution to a stationary problem with a nonhomogeneous boundary condition. These modes, makes it possible to extend the validity of the reduced model. It also makes it possible to use Reduced-model inputs in constraints for more general use in an Modal Reduced-Order model produced by the Model reduction.
(20-10)
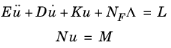
where E is the mass matrix,
D is the damping matrix,
K is the stiffness matrix, and
L is the load vector. Either
E or
D can be identically zero. Here
N is the constraint Jacobian and
M the constraint load vector. The modal solver algorithm requires that a few eigenvectors have been computed to the corresponding homogeneous harmonic problem. The eigenvalue solvers in COMSOL automatically considers the homogeneous problem when a formulation as the one above is used. That is, in its simplest form, it solves the eigenvalue problem
Several different constraint load vectors Mj can be used and thereby define several constraint modes. If you form a matrix
Φ whose columns are the eigenvectors and the constraint modes, then an approximation
um of the solution
u can be written as
(20-11)
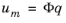
where q is a small vector of
m unknown coefficients. Replacing
u in
Equation 20-10 by
um and premultiplying by
ΦH yield
(20-12)
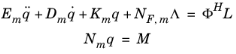
where Em = ΦHEΦ,
Dm = ΦHDΦ,
Km = ΦHKΦ,
Nm = NΦ, and
NF,m = ΦHNF.
The damping matrix D may be present when performing the eigenvalue analysis. It is, however, possible to add additional damping by providing damping ratios per mode (or one ratio for all modes). If
λi denotes the
ith eigenvalue and
ξi the associated damping ratio, then
is added to the ith diagonal entry of the reduced damping matrix in
Equation 20-12. If
E and
K are real and symmetric positive definite,
D = 0, and
Em and
Km are diagonal, then
ξi can be interpreted as the fraction of critical damping in the
ith mode.
The modal solver algorithm supports Model Control Inputs in the load vector and the constraint load vector. Denoting these inputs
ν, gives
where Br = ΦH∂L/∂ν,
Brdot = ΦH∂L/∂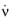
,
Brdotdot = ΦH∂L/∂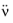
, and
BM = ∂M/∂ν.
(20-13)

be a vector of output variables, Y0 the output bias vector,
Cr the output matrix, and
F the feedback matrix.
The Modal Solver (using a
Time Dependent, Modal study step) and the
Time Dependent, Modal Reduced-Order Model, can export the reduced matrices and vectors for use in further simulations.
For time-dependent studies, the load L1 is assumed to be of the form
l(
t)
ΦHL0, where
L0 is constant, and
l(
t) is the given load factor. Further, the projection matrix
Φ is possibly appended with one or two columns such that the initial values
u(
0)
= u0 and

lie in the range of
Φ. These initial value vectors are appended before the constraint modes are appended
Φ.
so that y = u − ud is zero on the boundary (for
ν = 0) and
When using the reduced order model (see Modal Reduced-Order Model) it is possible to use the constraint modes rather freely. The default is that the constraint mode DOFs are constrained to be equal to a corresponding Reduced-model input expression
where qj is a constraint mode DOF connected to the model input expression
νk. The motivation for this behavior is that if the constraint modes fulfill the conditions
(20-14)
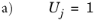
(20-15)
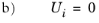
on the boundaries where i ≠ j, then the default boundary condition for the reduced model approximates the constraint
on the boundary ∂Ωj. Notice that this behavior can be modified from the Modal Reduced-Order Model node and the
Constraint Modes dialog. The map between the constraint mode number
i (not the DOF number) and the input expression index
k is exported as a vector
CImap(i) = k from the modal solver algorithm. This map returns -1 if there is no such expression.
The following reduced matrices can be exported: the mass matrix Em, the
damping matrix Dm, the
stiffness matrix Km, and the
damping ratio matrix
where p is the number of columns that were appended to
Φ (that is, the damping ratios do not affect the
p last diagonal entries coming from initial vectors or constraint mode vectors). Furthermore, the
load vector,
ΦHL0; the
input matrix Br; the
time derivative input matrix Brdot; the
second time derivative input matrix Brdotdot; the
output bias vector Y0; the
output matrix Cr; the
output feedback matrix F; the
stiffness matrix times ud,
ΦHKud; the
projection matrix,
Φ; the
constraint mode to input map,
CImap; the
initial value vector,
q(0); and the
initial derivative vector,

, can be exported.
For the frequency domain, COMSOL also supports linearized formulations as well as rather general formulations in terms of the frequency. The Equation 20-10 is linear and cannot be used to describe this. The starting point for the model reduction of a frequency-domain problem is a FEM residual vector expansion around a frequency
f0 = ω0/(2
π). Consider the unreduced residual vector expanded in a three term Taylor expansion
(20-16)

(20-17)

(20-18)
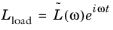
where ω is the angular frequency of the forcing function and the constraint load vector
Mload is assumed to be of the type
The solution to Equation 20-18 is on the form

, and we can again use the approximation
Φq(ω,t), where

, but as usual only the time-independent factor
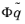
is returned by the solver or when reconstructed by the reduced-order model. Using this approximation in
Equation 20-18 and multiplying from the left with
ΦH, gives the reduced frequency-domain problem
(20-19)
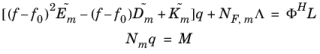
where the ~ notation is dropped for q,
Λ,
L, and
M from here on. We also introduce
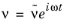
and drop the ~ notation. Here,
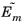
,
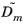
, and

are the reduced coefficient matrices from
Equation 20-18 and
is added to the sum inside the square bracket of Equation 20-19. Notice that when the coefficient matrices are independent of the frequency, this damping term coincides with what is added in the corresponding Time Dependent, Modal study.
(20-20)
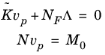
is then subtracted from the right side of Equation 20-19. Reduced-model inputs in constraints are handled very much like the time-dependent case. Constraint modes, computed as above for a Stationary problem, are supported. The produced reduced order model can rather freely constrain these reduced constraint mode DOFs. Also here the default behavior is to constrain these to their corresponding input expression
qj = νk, and also for the frequency domain this behavior can be modified from the Modal Reduced-Order Model.
From the Modal Solver and the
Frequency Domain, Modal Reduced-Order Model, the following reduced matrices can be exported: the
mass matrix,
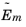
; the
damping matrix,
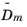
; and the
stiffness matrix 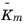
. The
damping ratio matrix,
Dratio; the
projection matrix,
Φ; the
mass matrix times the particular solution,

; the
damping matrix times the particular solution,
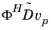
;and the
load vector 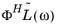
can also be exported. Furthermore, the
constraint mode to input map,
CImap; the
input matrix Br; the
time derivative input matrix Brdot; the
second time derivative input matrix Brdotdot; the
output bias vector Y0; the
output matrix Cr; the
output feedback matrix F; The exported load vector is assembled for the last given frequency
ω. You can also export all load vectors (that is,

,
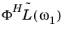
, …,
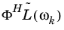
). This results in a matrix whose columns are all assembled load vectors. If
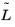
is independent of
ω, this matrix only contains one column.
|
|
To export the matrices, in the Modal Solver node’s Settings window, expand the Output section and then select the Solution or Reduced matrices check boxes to display check boxes for the various reduced matrices and vectors. Select the check boxes for the matrices and vectors that you want to export.
|
|
|
Modal in the COMSOL Multiphysics Programming Reference Manual.
|