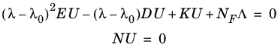The Eigenvalue Solver Algorithms

where the solver evaluates E, D, K, N, and NF for the solution vector U0; λ denotes the eigenvalue; and λ0 is the linearization point. If E = 0, it is a linear eigenvalue problem; if E is nonzero, it is a quadratic eigenvalue problem. To solve the quadratic eigenvalue problem, COMSOL Multiphysics reformulates it as a linear eigenvalue problem. After constraint handling, it is possible to write the system in the form Ax = λBx.

More general eigenvalue problems sometimes arise when boundary conditions or material properties are nonlinear functions of the eigenvalue. These cases can be handled as a series of quadratic eigenvalue problems. COMSOL Multiphysics treats general dependencies on the eigenvalue by assembling a quadratic approximation around the eigenvalue linearization point λ0. Normally, iteratively updating the linearization point leads to rapid convergence.

Finding the eigenvalues closest to the shift σ is equivalent to computing the largest eigenvalues of the matrix C = (A − σB)−1B. To do this, the solver uses the ARPACK FORTRAN routines for large-scale eigenvalue problems (Ref. 13). This code is based on a variant of the Arnoldi algorithm called the implicitly restarted Arnoldi method (IRAM). The ARPACK routines must perform several matrix-vector multiplications Cv, which they accomplish by solving the linear system ( A − σB) x = Bv using one of the linear system solvers.

The eigenvalue region method uses an algorithm based on ARPACK that makes it possible to find all eigenvalues within a given, sufficiently small region (rectangle) in the complex plane. The algorithm uses ARPACK to find eigenvalues covering a rectangle in the complex plane containing the sought eigenvalues; that is, there are eigenvalues with real or imaginary parts larger and smaller than the given smallest and largest real or imaginary parts. In an optional consistency check, a Schur basis corresponding to the found eigenvalues is used as input to ARPACK for a search for an additional eigenvalue. The initial vector is taken to be orthogonal to the Schur basis. If the new eigenvalue falls outside the rectangle spanned by the eigenvalues previously found, the algorithm uses this information as an indication that all desired eigenvalues are found and the algorithm terminated successfully. The algorithm uses the following inputs:

The shift is taken as the center of the rectangle of sought eigenvalues.

The eigenvalue region method starts by searching for the given approximate number of eigenvalues. If the converged eigenvalues cover the sought region, it may perform an optional consistency check where it searches for an additional eigenvalue using a Schur basis corresponding to the found eigenvalues covering the sought region and an initial vector guess orthogonal to this basis as input to ARPACK. If the new eigenvalue lies outside the covering rectangle, the algorithm terminates successfully, and the eigenvalues within the sought region are returned. If the new eigenvalue lies inside the covering rectangle, there may be additional eigenvalues within the sought region, and a warning is issued to decrease the region where eigenvalues are sought.

If the converged eigenvalues do not cover the sought region, the number of eigenvalues searched for is doubled. The window then shows Searching for more eigenvalues. If the number of eigenvalues searched for has already been doubled and no additional eigenvalues have been found within the region, a warning is issued. The warning shows, for example, that no (transformed) eigenvalue with a smaller real part is found. It is then advised to decrease the size of the region where you want to search for eigenvalues.

The number of eigenvalues sought for can be reduced by the algorithm if the given approximate number of eigenvalues is found to be larger than the number of eigenvalues inside and close to the sought region. The Log window then shows Searching for fewer eigenvalues.

With the option , COMSOL Multiphysics uses a LAPACK algorithm for finding all eigenvalues and eigenmodes using a filled system matrix for small eigenvalue problems.

The FEAST eigenvalue solver can be understood as an accelerated subspace iteration combined with the Rayleigh–Ritz procedure (Ref. 20). It calculates the eigenpairs whose eigenvalues lie in a specific region defined in the complex plane.

The accelerator, which is defined as the integral along a complex contour C

can also be seen as a filter or a spectral projector that maps all unwanted ones to 0 and all wanted eigenvalues (inside the contour C) to 1 (Ref. 18).

FEAST first projects a random selected initial subspace X(0) onto the subspace spanned by the eigenvectors of interest and then uses the Rayleigh-Ritz procedure in this subspace to extract eigenvalue/eigenvector approximations. Projection onto the subspace of interest is accomplished by

(See also Ref. 19).The integration in Equation 20-8 is approximated by a numerical quadrature with appropriate integration points and weights.

Where zj and ωj are integration points and weights, respectively, and each Qj is obtained by solving shifted linear systems (zjB − A) Qj = BX(0). The resulting subspace Q is then orthogonalized and used in the Rayleigh–Ritz procedure. By repeatedly applying the projection in Equation 20-9, the orthogonalization Q, and the Rayleigh–Ritz procedure, FEAST refines the estimates for the eigenvectors of interest.