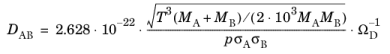The Reaction Engineering Interface and The Chemistry Interface can calculate several transport properties that can be accessed in interfaces in space dependent models.

The diffusion coefficients are calculated from the following expression based on kinetic gas theory (Ref. 7):

Here, DAB (SI unit: m2/s) is the binary diffusion coefficient, M (SI unit: kg/mol) equals the molecular weight, T (SI unit: K) represents the temperature, p (SI unit: Pa) is the pressure, and σ (SI unit: m) equals the characteristic length of the Lennard-Jones/ Stockmayer potential. In addition, ΩD is the collision integral, given by the relation of Neufeld et al. (Ref. 6):

In Equation 2-62, cx are empirical constants, μD is the species dipole moment value (SI unit: Cm) and ε/kb (SI unit: K) the potential energy minimum value divided by Boltzmann’s constant. Tabulated data in literature frequently lists values of ε/kb rather than ε. It should be noted that predefined expressions for binary diffusivities only treat ideal gas mixtures. Thus, these are applicable as input only for gases at moderate pressure in multicomponent diffusive transport models.

The binary diffusivity according to Equation 2-61 is also suited for gaseous species in solvent, simply by setting either the component A or B to the solvent. The binary diffusion coefficient is in this case equal to the diffusion coefficient of the bulk species.

The diffusivity of a species A in a solvent B is calculated with the Wilke–Chang equation (Ref. 8):

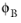
where μB (SI unit: N·s/m2) denotes the solvent’s dynamic viscosity (see Equation 2-69), and Vb,A (SI unit: m3/mol) equals the molar volume at the normal boiling point of the solute species. is the dimensionless association factor of the solvent, which by default is set to 1.

The dynamic viscosity of the mixture is assumed to be the same as that of the solvent. This is given by the kinetic gas theory (Ref. 6 and Ref. 7), with species i being the solvent:

In Equation 2-65, μ (SI unit: Ns/m2) represents the dynamic viscosity, and ΩD is the dimensionless collision integral given by:

In Equation 2-65 and Equation 2-66, bx are empirical constants, μD (SI unit: Cm) the species dipole moment value, and ε/kb (SI unit: K) the potential energy minimum value divided by Boltzmann’s constant. Tabulated data in literature frequently lists values of ε/kb rather than ε, and σ (SI unit: Å) is the characteristic length value.

The dynamic viscosity of gas mixtures without solvent are calculated according to Ref. 9 with the following expression:

where φij is defined as:

In Equation 2-67 and Equation 2-68, xi is the molar composition and μi is computed with Equation 2-65 for each of the species in the mixture.

The dynamic viscosity of the mixture is assumed to the same as that of the solvent. An approximate expression for the temperature dependence of the dynamic viscosity is given by (Ref. 3):

where μ (SI unit: Ns/m2) is the dynamic viscosity. As inputs for Equation 2-69, the physics interface takes the reference viscosity, μref (SI unit: Pa⋅s) at the reference temperature Tref (SI unit: K).

The predefined expression for thermal conductivity comes from the Stiel–Thodos equation (Ref. 10), which is defined as:

where k (SI unit: W/(m·K)) is the thermal conductivity and Cp (SI unit: J/(mol·K)) denotes the molar heat capacity. Equation 2-70 is a function of viscosity, μ, as given by Equation 2-65. Equation 2-70 is directly used in the case of a solvent; all parameters being those of the solvent. Without a solvent, however, the following equation is also used:

where ki is the thermal conductivity of each species i and xi the molar composition for each of the species in the mixture.