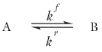
According to Equation 2-2 the reaction rate (SI unit: mol/(m
3·s)) is formulated as:
where cA and
cB (SI unit: mol/m
3) are the concentrations of
A and
B, and
kf and
kr (SI unit: 1/s) are the forward and reverse rate constants, respectively. The net rate expressions with respect to species
A and
B are then:
Assuming the reaction in Equation 2-30 is at equilibrium, the reaction rate
r is 0:
The rate of consumption of species A equals the production rate of species
B, as shown in
Equation 2-32 and
Equation 2-33.
With the combined information in Equation 2-32,
Equation 2-33, and
Equation 2-31, the Reaction Engineering interface is able to define the mass balances for the equilibrium system without the reaction rate expressions. The equation system solved for becomes:
In general, for a system of reactions contributing to k mass balances and with
j reactions being at equilibrium, the reduced system of equations to be solved is composed of
k – j mass balances and
j equilibrium expressions. The elimination process producing the above system of equations is automated, allowing simple modeling of chemical equilibrium reactions together with irreversible and/or reversible reactions.
Now compare Equation 2-37,
Equation 2-38, and
Equation 2-39 with the balance equations that the physics interface sets up for the related chemistry, where the second reaction is instead an equilibrium reaction:
In contrast to the reversible reaction given by Equation 2-36, to make use of the information contained in the equilibrium relation, the mass balances must be reformulated. Mass balances set up for the reactions given by
Equation 2-40 and
Equation 2-41 are then:
The equilibrium expression (Equation 2-43) introduces an algebraic relationship between the species’ concentrations.