The Equilibrium Constant
In general, chemical equilibrium is reached when the Gibbs free energy of the system is minimized. The Gibbs free energy of is defined as
(2-6)
where U is the internal energy, P is pressure, V is volume, T is temperature, S is entropy and H is enthalpy of the system. For a closed system
(2-7)
where δQ is (reversible) heat transfer to the fluid and δW is (pressure) work in the system. The change in Gibbs free energy can be written as
(2-8)
Chemical potential μi is defined as partial molar Gibbs energy for species
(2-9)
where n is the number of mole of species i in the system. At constant temperature, this expression can be integrated as a function of pressure
(2-10)
where v is molar volume and is chemical potential of species at standard state. For an ideal gas this can be expressed as
(2-11)
The equilibrium criterion can be written as
(2-12)
where νi is the stoichiometric coefficient and μi is the chemical potential of species i in the reaction. We can evaluate the chemical potential as partial molar Gibbs energy of species in mixture as
(2-13)
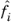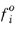
where is the fugacity of species i in the mixture, and is the fugacity of pure species in the standard state. Equation 2-12 can be rewritten as
(2-14)
The equilibrium constant for the reaction, K, is defined as
(2-15)
where ai is the activity of species in the system.
is the Gibbs free energy of reaction (including formation terms) which is defined, in accordance with Equation 2-6, as
(2-16)
the enthalpy of reaction, , and entropy of reaction, , both at a given temperature T is defined as
(2-17)
(2-18)
Here is the temperature at standard state. and are the standard enthalpy of formation and absolute entropy for each species (these data are available in the COMSOL database).
Activity
Activity of species, ai is defined by Equation 2-13 as
(2-19)
Activity depends on the choice of an arbitrary standard state. The standard state of pure species is usually at 105 Pa and for solute in solution is based on hypothetical molality or amount concentration also referred as infinite dilute behavior.
The activity of a species in a mixture is expressed by relationship between dimensionless activity coefficients, γi, and measured amount of the species in the system.
(2-20)
Activity coefficients are usually estimated by Activity coefficient models.
Gas phase
The standard state is the pure species at ideal gas condition, 1 atm and the equilibrium temperature. Activity of species in mixture is expressed by:
(2-21)
where and are fugacity and fugacity coefficient of species i in the mixture.
Liquid phase
The standard state is pure liquid species at 1 atm and equilibrium temperature. The fugacity of a species in a mixture is given by
(2-22)
where γi is the activity coefficient of species in the mixture and fi is the fugacity of pure species at the equilibrium temperature and pressure. The activity is expressed by
(2-23)
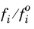
where fio is the fugacity of pure species at the equilibrium temperature and 1 atm. The ratio is given by
(2-24)
where 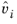is the partial molar volume of species and Psat is species saturated vapor pressure. For liquids is weak function of pressure and can be assumed to be 1 unless at high pressure.
Dilute Solutions
The concentration can in the case of non-ideal mixtures be replaced with the activity. In these interfaces, the dimensionless activity (ai) depend on species concentration (ci), activity coefficient (γi) and the standard state concentration (c0s=1 mol/m3).
(2-25)
Additionally, an effective species concentration (ce,i) (SI unit: mol/m3) is used in the reaction rates (Equation 2-2) when activities are utilized.
(2-26)
Automatically Defined Equilibrium Constants
Below the automatically defined equilibrium constants are defined in terms of the equilibrium expression Keq
(2-27)
Gas Phase
Inserting Equation 2-21 in Equation 2-15 gives:
(2-28)
where for ideal mixtures, the fugacity coefficients are equal to 1.
Liquid Phase
For low and moderate pressure, the equilibrium constant can be reformulated by substitution of Equation 2-23 to Equation 2-15 as:
(2-29)