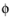
The ternary phase field model implemented in COMSOL is based the work of Boyer and co-workers in Ref. 2. The model is designed in order to study the evolution of the three immiscible phases, denoted phase A, phase B, and phase C, respectively. Each phase is represented by a phase field variable , which takes values between 0 and 1. The phase field variables satisfies the constraint

Here the σij denotes the surface tension coefficient of the interface separating phase i and j, and the capillary parameters Σi are defined as

and Λ is a function or parameter specifying the additional free bulk energy. By default Λ is zero. In this case it can be seen that the free energy in Equation 11-30 represents the mixing energy, since only interfaces between two phases (where two phase field variables varies between the limiting values) contributes to the free energy.

The Cahn-Hilliard equations to be solved for each phase p = A, B, C are

It can be noted that the Cahn-Hilliard equation is originally a 4th-order PDE. In COMSOL Multiphysics, that PDE is split up into two second-order PDEs by introducing an additional dependent variable, the generalized potential η, one for each phase. In order to satisfy Equation 11-30, two sets of the equations shown in Equation 11-32 are solved, those for phase A and phase B. The phase field variable, and correspondingly the mass fraction, for fluid C is computed from Equation 11-30.

In Equation 11-32 ε (SI unit: 1/m) is a parameter controlling the interface thickness, M0 (SI unit: m3/s) is a molecular mobility parameter, and the parameter ΣT is defined as