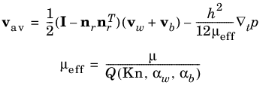Flow Models for Rarefied Gases
For gases at low pressure, the ratio of the gas mean free path, λ, to the gap size (known as the Knudsen number: Kn = λ/h) grows. For Knudsen numbers greater than 0.1, the gas cannot be treated using the continuum Navier–Stokes equations, and the Boltzmann equation must be solved instead.
At steady state, the solutions to the linearized Boltzmann equation for isothermal flow in a narrow gap between parallel plates can be expressed as a combination of Poiseuille and Couette flows. This is analogous to the solutions of the Navier–Stokes equations in the limit of small h0/l0.
Provided that the wall and base surfaces are identical (which is normally the case in many practical applications), the Couette contribution to the bulk fluid velocity is unchanged (it remains the mean of the wall and base velocities for identical surfaces).
The Poiseuille contribution to the flow is more complicated for rarefied gases. A practical approach, pioneered by Fukui and Kaneko (Ref. 4) is to solve the linearized Boltzmann BGK equation over a range of Knudsen numbers and to provide an empirical fit to the flow. This results in the following form for the average flow velocity:
(9-11)
where Q(Kn, αw , αb) is a nondimensional function of the Knudsen number (Kn), and the tangential momentum accommodation coefficients at the wall and base (αw and αb).The function Q(Kn, αw , αb) is obtained by solving the linearized Boltzmann BGK equation for steady Poiseuille flow with a range of Knudsen numbers and slip coefficients. This approach assumes that stationary solutions of the Boltzmann equation apply inside the gap, that is, that the flow can be treated as quasi static.
In Ref. 5 there is data for Q(Kn, αw , αb) in the case where αw = αb, which was subsequently fitted to different empirical formulas by Veijola and others (Ref. 6). Note also that additional and more accurate data is available in Ref. 7. In Ref. 6 there are two empirical formulas, which apply under different circumstances with various degrees of accuracy:
•
αw = αb = 1 (available as the option Rarefied-total accommodation):
which is accurate to within 5% in the range 0 < Kn < 880.
•
αw = αb = α (available as the option Rarefied-general accommodation):
which is accurate to within 1% in the ranges 0.7 < α < 1, and 0.01 < Kn < 100.
Both of these empirical models are available as flow models. Additionally, a user defined relative flow rate function Q can be defined for Equation 9-11, which could be based on an interpolation data as described in Ref. 7. Data on the tangential momentum accommodation coefficients for various gas-surface combinations is also available in Ref. 2.
Various definitions of the mean free path are used in the literature, frequently without explanation. For compatibility with the existing literature on thin-film flow, COMSOL Multiphysics uses the same mean free path definition as in Ref. 6.
In Ref. 6 the mean free path and Knudsen number are defined as:
(9-12)
where μ is the gas viscosity, p is the gas pressure, R is the molar gas constant, T is the temperature, and Mn is the molar mass of the gas. Ref. 2 also employs this definition of the mean free path.
In many applications the forces acting on the wall and base are important. The pressure in the gas can be computed correctly by solving Equations 9-10 and 9-11. However, this approach provides only the normal component of the traction acting on the wall and base. To obtain the shear forces, the approach adopted by Torczynski and Gallis (Ref. 8) is used. They produced an empirical expression for the shear force that has the correct behavior in the free molecular flow and continuum limits as well as in the limits for the accommodation coefficient. Torczynski and Gallis solve the problem of pure Couette flow and derive an empirical function for the slip length that predicts the correct forces for the flow in the gap in several limiting cases. Their empirical expression for the slip length is given by:
(9-13)
where d1 ≈ 0.15 and d2 ≈ 0.59. In principle d1 and d2 are variables themselves, but they were found to be constant to within the accuracy of the DSMC experiments used to derive their values.
The slip length in Equation 9-13 (which is used in COMSOL Multiphysics) differs slightly from the equivalent expression in Ref. 8 as a result of a different definition of the mean free path (Torczynski and Gallis’ mean free path is different from Equation 9-12 by a factor of √π/2).
Equation 9-7 gives the following expressions for the shear forces on the wall and base for pure Couette flow:
where Ls is taken from Equation 9-13.
A general flow incorporates both Poiseuille and Couette terms. Assuming that the Poiseuille and Couette flows can be superposed, the forces become:
(9-14)
here Ls is derived from Equation 9-13 and p is obtained by solving Equation 9-10 with Equation 9-11. Strictly speaking, Torczynski and Gallis’ results apply for Couette flow only, and were derived for a more general variable-soft-sphere gas rather than for the linearized BGK equations. From a practical perspective, it seems likely that solutions of the linearized BGK equations would also be fitted by these expressions, and in that case it could be possible to combine the forces using superposition. In the absence of a detailed proof, Equation 9-14 is not the default option for the force model, but it is available as an additional option.
Both Ref. 6 and Ref. 7 provide data for the relative flow rate Q(Kn, σsw, σsb) in specific cases where the wall and base have different accommodation coefficients. Since no details on how to compute the forces acting on the walls for highly rarefied gases were published, these models are not currently supported in COMSOL Multiphysics.