Synthetic Turbulence Inlet Condition

The methodology used for generating turbulent, fluctuating velocity field at the inlet boundary using Fourier series is described. A time correlation between such fields generated at successive time instances is provided.

An instantaneous, turbulent, fluctuating velocity field,

, is generated at each time step of the simulation using random Fourier modes as

Here, N is the number of Fourier modes in the wave number space κmax − κmin. This space is divided into intervals of size Δκ = (κmax − κmin)/(N − 1). The largest wavenumber, κmax, is taken to be 2π/Δ, where Δ is the smallest element size in the inlet boundary, disregarding the boundary layer elements. The smallest wavenumber, κmin, is taken to be κe/p. Here, p = 5 is chosen as a suitable value and κe = (9πα)/(55LT), where α = 1.453, the turbulent length scale LT = (Cμ3/4k03/2)/ε0, and Cμ = 0.09 is the default value.

The quantity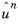

is the amplitude of the nth mode. It is obtained from a modified von Karman spectrum as,

The quantity κη = ε01/4ν−3/4, where, ν is the fluid kinematic viscosity. The root mean square velocity is calculated as

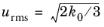
. The components of the wavenumber vector for the nth mode are computed from random angles θn and

as,

The random angles are generated at each time step and for every Fourier mode such that the wave number vectors are uniformly distributed in the hemispherical shell, that is, 0 ≤ θn ≤ 2π and

. Additionally, the user may specify a seed value to be used in the generation of the random angles.

The phase angle βn = κn·x + ψn, where the phase angle at the origin, ψn, is randomly generated, such that, 0 ≤ ψn ≤ 2π.

The direction of the fluctuating velocity, σn, is chosen to be orthogonal to the wavenumber vector. Its orientation in the plane orthogonal to the wavenumber vector is determined by a random angle αn, where 0 ≤ αn ≤ 2π. It is given as,

At each time step, an instantaneous velocity field is generated as described in the previous section. Such velocity fields generated at successive time instances are totally independent of each other. To overcome this non-physical nature of the fluctuations, the following correlation in time is introduced. It provides a convenient way to prescribe the turbulent time scale of the fluctuations.

The fluctuating component of the prescribed inlet velocity at current time,

, and the instantaneous velocity fluctuation,

, as

The coefficients c1 = exp(−Δt/Tint) and

. Here, Δt is the time step size. The integral time scale is computed as Tint = Lint/Ub, where the integral length scale, Lint, is given by k03/2/ε0 and the bulk velocity, Ub, is the norm of the velocity averaged over the inlet boundary.