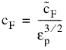You are viewing the documentation for an older COMSOL version. The latest version is
available here.
Since Darcian flow is not compatible with the character of a turbulent flow, only
Non-Darcian flow is available in
Porous Medium domains as a
Flow model option when a two-equation turbulence model is activated. The turbulence equations are fully active in a
Porous Medium and are modified according to the theory below. Currently, the algebraic turbulence models do not change the formulation of the momentum equation in porous domains and the Spalart-Allmaras model prohibits them.
A detailed description of turbulence in porous media can, in principle, be achieved by employing common turbulence modeling in the corresponding complex geometries. However, heavy computations would be needed when a characteristic size of the porous matrix cavities, or pores, is much smaller than the geometry dimensions. A characteristic size of the pores, the porous length scale, is given by 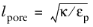 , where κ
, where κ and
εp are the medium’s permeability and porosity, respectively. For this reason, a simplified framework for turbulence modeling in porous media has been developed. It is based on taking the turbulence equations in the interstitial space and averaging them over the whole combined volume of fluid and porous matrix (
Ref. 30), a so called Representative Elementary Volume (REV). In such a way a detailed information about gradients of velocity and other quantities on the
lpore-scale is not available, but its influence is modeled by introducing extra terms which depend on the REV-smoothed quantities.
(3-169)
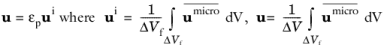
Here 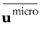 is Reynolds-averaged microscopic velocity, ΔV
is Reynolds-averaged microscopic velocity, ΔV is the REV-cell volume (large enough to guarantee sufficient smoothing, but not larger than a fraction of the mean gradient scale) while
ΔVf is the fluid part of the REV-cell,
u is the REV-averaged mean velocity (mean Darcy velocity, or volume flow velocity, essentially) and
ui is the REV-averaged mean interstitial velocity. Note that for all our purposes it is sufficient to define
ui as
ui = u/εp. For the velocity gradients we assume
(3-170)
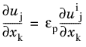
where deviations from this expression (Ref. 30) are lumped into the modeled extra contributions. Turbulence kinetic energy and turbulence dissipation rate obey the same averaging and scaling rules as mean velocity
(3-171)
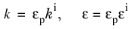
(3-172)
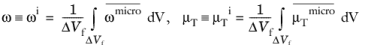
This happens because ω and
μT do not have a reasonable volumetrically spread interpretation. Next, turbulence friction velocity is scaled by definition as
(3-173)
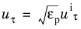
(3-174)
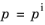
(3-175)
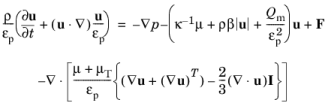
The formal modification of the k-equation involves changing convective term as
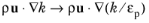
and adding production by the porous matrix
Pk,pm to the shear production
Pk → Pk + Pk,pm
(3-176)
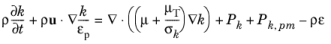
(3-177)
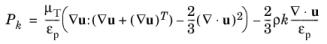
For ε−equation the changes are completely analogous: convective term is modified according to
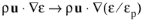
and turbulent dissipation rate production by the porous matrix
Pε,pm is added to the right-hand side
(3-178)
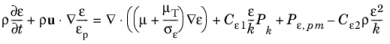
For ω-based models the convective term changes as
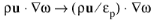
and turbulent specific dissipation rate production by the porous matrix is added
Pω,pm
(3-179)
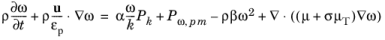
The above modifications have been illustrated for the k-
ε model and
ω-equation of the
k-
ω model, but are generally applicable to any two-equation turbulence model.
(3-180)
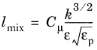
(3-181)
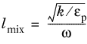
The realizable k-
ε model needs redefinition
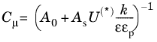
.
For the k-
ω model
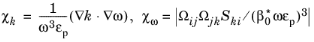
. Analogously,
The modifications to the ζ-equation of the v2-f model are the following: change convective term as
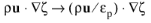
, change
Pk → Pk + Pk,pm in both terms on the right-hand side which contain
Pk, and limit variable
L by
lpore
(3-182)
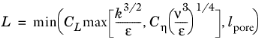
Wall Distance is now computed treating
Wall and
Interior wall adjacent to porous domains as usual solid walls.
Porous medium turbulence model complements a basic turbulence model providing modeling for the above declared terms
Pk,pm and
Pε,pm, and
Pω,pm. The available modeling approaches are:
Default,
Nakayama–Kuwahara, and
Pedras–de Lemos.
Default and
Nakayama–Kuwahara (
Ref. 31) employ the following form of the porous production
Pk,pm of turbulence kinetic energy
(3-183)
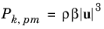
(where β is the non-Darcian coefficient from the Brinkman equation) while
Pedras-de Lemos (
Ref. 30) relies on
(3-184)
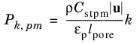
For ε-based equations,
Default and
Pedras-de Lemos model the turbulence dissipation rate
Pε,pm as
(3-185)
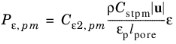
while Nakayama–Kuwahara gives
(3-186)
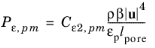
For the k-
ω and SST models,
Default and
Pedras–de Lemos model porous production of the specific turbulent dissipation rate
Pω,pm as
(3-187)
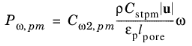
while Nakayama–Kuwahara as
(3-188)
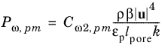
For ε-based models
Cε2,pm is always the corresponding
Cε2 coefficient entering
ε-equation (that is
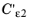
for v2-f ).
Default and
Pedras-de Lemos have
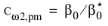
for k-
ω and
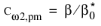
for SST, while
Nakayama–Kuwahara has
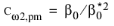
for k-
ω and
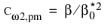
for SST.
Essentially, Default uses
Pk,pm in the form proposed by Nakayama–Kuwahara and
Pε,pm or
Pω,pm in the form proposed by Pedras–de Lemos. Since
ρβ|u|3 essentially is turbulence dissipation in the porous matrix,
Default and
Nakayama–Kuwahara are conservative models so that the
k-equation guarantees that in a dense porous medium the specific turbulence dissipation achieves its limiting value
(3-189)
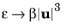
The ε-equation, and
ω-equation, of all the three models as well as the
k-equation of Pedras-de Lemos ensure that the turbulence frequency in a dense porous matrix would approach its limiting value
(3-190)
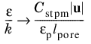
Thus, Default and
Nakayama–Kuwahara also ensure that in a dense porous matrix
(3-191)
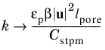
However, Pedras–de Lemos then becomes a degenerate model with two identical equations, and the limiting values of
k and
ε might depend on the initial and boundary conditions in an uncontrollable way.
The coefficient Cstpm, which we call a
Coefficient of subgrid turbulence generation by porous matrix, is equal to 0.212 by default as given in
Ref. 31. However for
Pedras-de Lemos it can be set to predefined
Original value
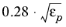
or
Recalibrated value 0.18. Both are based using
Equation 3-190 to match limiting values of
ε/k, obtained using pore resolving simulations in dense porous matrix at different
εp, with
Cstpm.
Original refers to
Ref. 30 usage
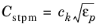
while
Recalibrated refers to the current convention when
Cstpm is considered as independent of porosity.
Wall treatment essentially inherits wall treatment of a corresponding basic turbulence model. The main modification is due to the need to determine if at δw =
hw/2 the turbulent log-layer still dominates (pores are resolved) or the limit of the dense porous matrix is reached (pores not resolved). The intermediate cases should be blended properly. In the current approach it is achieved by introducing an indicator function
indpmLL,which quantifies porous matrix dominance over the log-layer and is modeled as
(3-192)
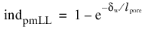
(3-193)
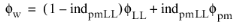
(3-194)
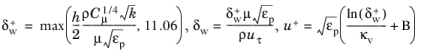
where for the Realizable k-
ε 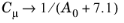
and for
k-
ω 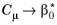 (
(also in expressions below
), while expression for the friction velocity
uτ is the same, and the traction is
(3-195)
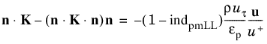
(3-196)
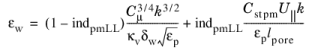
(3-197)
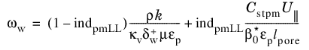
Now uτlog and
δw+ are modified as
(3-198)
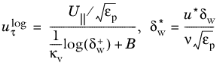
while the definitions of uτvisc,
u∗, log,
uτ, and
u∗ remain the same.
(3-199)
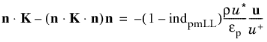
(3-200)
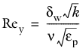
(3-201)
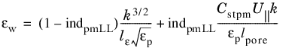
For v2-f model the further modifications are
(3-202)
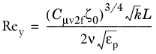
(3-203)
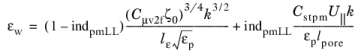
For k-
ω and SST models
ωvisc does not change and the further modifications are
(3-204)
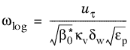
(3-205)
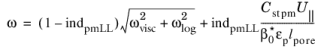
Low Reynolds number treatment is formally identical to the usual clear flow Low Re treatment. Strictly speaking, it is applicable only in case if the pore cell is fully resolved by the mesh. Otherwise the first computational cell is in the porous matrix but common clear flow
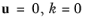
conditions are applied. Thus, the behavior in several near-wall cells would be not correct.
The two definitions of the production of turbulence kinetic energy by buoyancy, User defined and
Automatic from multiphysics, become modified in porous domains as
(3-206)
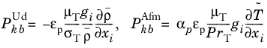
(3-207)
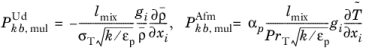
All the equations in porous medium presented above can be rewritten in terms of the mean interstitial quantities 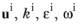 . If we assume constant εp
. If we assume constant εp and multiply
k-equation and
ε-equation by
εp, then porosity
εp would disappear from all the equations and they would look identical to the original clear flow equations. The additional terms (Darcy and Forchheimer in the momentum equation, and the above introduced extra productions in the turbulence equations) would contain the geometrical information about porous medium only via
lpore. This reasoning is naturally extended to all the boundary conditions. Also, all the numerous non-dimensional intermediate variables which enter turbulence equations, for example
Rt in the Low-Re
k-
ε model, should be scaled properly. Then, since scaling does not effect length and time, all the intermediate lengths, frequencies and viscosities should be physical.
(3-208)