This is a normal stress condition together with a no-tangential-stress condition. When μ > 0, Equation 3-30 or Equation 3-31 can be supplemented with a tangential velocity condition

If so, the no-tangential-stress condition is overridden. An issue with Equation 3-30 or Equation 3-31 is that it does not strongly enforce unidirectional flow on the boundary. If the prescribed pressure on an outlet is too high, parts of the outlet can actually have inflow. This is not as much of an issue for the Navier–Stokes equations as it is an issue for scalar transport equations solved along with the Navier–Stokes equations. Hence, when applying the Pressure boundary condition at an outlet or inlet you can further constrain the flow. With the Suppress backflow option

Equation 3-33 effectively means that the prescribed pressure is p0 if u⋅n ≥ 0, but smaller at locations where u⋅n < 0. This means that Equation 3-33 does not completely prevent backflow, but the backflow is substantially reduced. Backflow is suppressed also when external forces are acting on the fluid, provided the magnitude of these forces are of the same order as the dynamic pressure at the outlet.

together with the tangential condition in Equation 3-32, or, a general flow direction is prescribed.

For incompressible single-phase flow, it is also allowed to specify the total pressure, ptot, instead of the static pressure, pstat, on inlet and outlet boundaries. It is more useful, for example, in pump applications. The pressure is then prescribed at the boundaries using Bernoulli’s principle,

The equation is imposed with two options: Average and Pointwise.

In the first option, pstat is prescribed by:

where ptot and |u|2 are averaged over the boundaries using the aveop operator:

For the second option, Equation 3-37 is prescribed pointwise.

See Inlet, Outlet, Open Boundary, and No Viscous Stress for the individual node settings. Note that some modules have additional theory sections describing options available with that module.
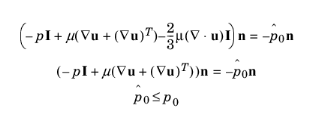