The current versions of the Nonisothermal Flow, LES interfaces only support incompressible flow. When gravity is active in the model, buoyancy effects may be taken into account using The Boussinesq Approximation. For large eddy simulations (LES) of nonisothermal flow, the temperature field is divided up into resolved and unresolved scales,
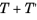
in the same way as is done for the velocity and pressure fields (see
Theory for the Large Eddy Simulation Interfaces). For incompressible flow, the energy equation can be projected onto the resolved scales,
w, producing the following weak form equation,
where q is the inward heat flux on the boundary
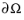
of the spatial domain
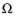
. The unresolved temperature scales are modeled in terms of the residual to the energy equation and the intrinsic time-scale,
Here, C4 is a constant depending on the shape of the element and
G is the covariant metric tensor.
where ρ is the fluid density,
Cp is the fluid heat capacity,
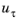
is the friction velocity and
T+ is the dimensionless temperature, given by,
E and
κ are the L-VEL parameters used in the automatic wall treatment expressions (see
Automatic Wall Treatment).